Uitwerking opgave 10 Exponentiële functies en grafieken

Terug naar Opgaven Exponentiële functies en grafieken

Opgave 10

Voor welke waarde(n) van $p$ hebben de functies:

$f:y=2^x$

$g: y=-(\displaystyle\frac{1}{2})^x+p$

slechts een punt gemeen.

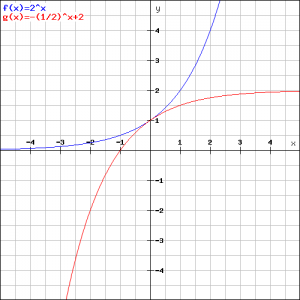
Teken voor de berekende waarde(n) van $p$ de grafieken van $f$ en $g$ .

Uitwerking

Om de snijpunten van $f$ en $g$ te berekenen, moeten we de volgende vergelijking oplossen:

$2^x=-(\displaystyle\frac{1}{2})^x+p$

$2^x=-2^{-x}+p$

$2^{2x}=-1+p2^x$

$2^{2x}-p2^x+1=0$

Door te stellen:

$z=2^x$

krijgen we de schaduwvergelijking:

$z^2-pz+1=0$

Deze tweedegraads vergelijking heeft twee samenvallende oplossingen als de discriminant $D=0$ , dus als:

$D=p^2-4=0$

$p=2$ of $p=-2$

Als $p=-2$ dan krijgen we $z=-1$ , dat wil zeggen $2^x=-1$ en dat levert geen oplossing op. De waarde van $p$ waarvoor beide grafieken slechts een gemeenschappelijk punt hebben is dus $p=2$ .

Ga vervolgens zelf na dat het gemeenschappelijke punt is $(0,1)$ . Zie ook de figuur.

Terug naar Opgaven Exponentiële functies en grafieken

Wiskunde
1. Basisboek Wiskunde.
door: Jan van de Craats en Rob Bosch (2e ed).
Een veel aangeraden boek dat vaak minder geschikt wordt gevonden voor zelfstudie.
2. Essential Mathematics for Econonomics and Business.
door: Bradley and Patton (4th ed).
Wordt gebruikt op de Erasmus Universiteit Rotterdam.
3. Essential Mathematics for Economic Analysis
door: Sydsaeter and Hammond (4th ed).
Degelijk boek dat wordt gebruikt op de Erasmus Universiteit Rotterdam.
4. Calculus: Concepts and Contexts.
door: Stewart (2nd ed).
Gaat wat dieper op de stof in dan de andere boeken.

Statistiek
Statistics for Management and Economics. Gerald Keller, Cencage Learning, 10th edition.

0

Web Design Bangladesh Web Design Bangladesh Mymensingh