Return to Assignments Exponential functions and graphs
Assignment 10
For which value(s) of ![]() do the graphs of the functions:
do the graphs of the functions:
![]()
![]()
have only one point in common.
Solution
In order to calculate the intersection points of ![]() and
and ![]() we have to solve the following equation:
we have to solve the following equation:
![]()
![]()
![]()
![]()
Substituting:
![]()
in the equation we get:
![]()
This quadratic equation has two coinciding solutions if the discriminant ![]() , so if:
, so if:
![]()
![]() or
or ![]()
If ![]() we get
we get ![]() , i.e.
, i.e. ![]() and this does not give a solution. Thus the value of
and this does not give a solution. Thus the value of ![]() for which both graphs have just one common point is
for which both graphs have just one common point is ![]() .
.
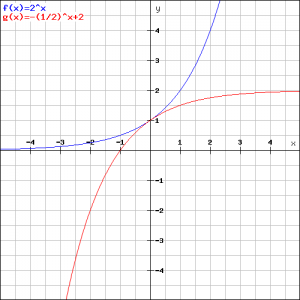
Verify that the common point is ![]() , see the figure.
, see the figure.