Terug naar Opgaven Logaritmische functies en grafieken
Opgave 7
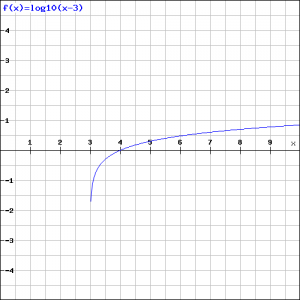
Teken de grafiek van de functie:
Uitwerking
De functie bestaat als beide logaritmen bestaan.
De eerste bestaat voor 
, dus voor 
of 
. We kunnen dit vaststellen omdat de kwadratische functie kan worden ontbonden in factoren:
De tweede logaritme bestaat voor , dus de functie bestaat voor .
De functie kan nu worden geschreven als:
![y=\log[(x-4)(x-3)]-\log(x-4)](https://4mules.nl/wp-content/ql-cache/quicklatex.com-d8c76a58c3aa3d37a0a576983ce2bf31_l3.png "Rendered by QuickLaTeX.com")
De grafiek van deze functie is veel eenvoudiger te schetsen dan die van de oorspronkelijke functie maar de grafiek is slechts geldig voor :
Terug naar Opgaven Logaritmische functies en grafieken
