Solution assignment 07 Logarithmic functions and graphs

Return to Assignments Logarithmic functions and graphs

Assignment 7

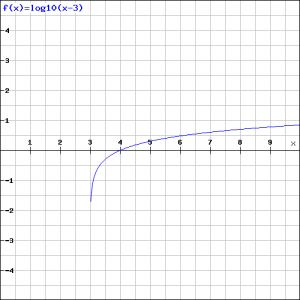
Draw the graph of the function:

$y=\log(x^2-7x+12)-\log(x-4)$

Solution

The function exists if both logarithms exist. The first is defined for $x^2-7x+12>0$ , thus for $x>4$ or $x<3$ . We know this because the quadratic function can be factorized:

$x^2-7x+12=(x-4)(x-3)$

The second logarithm is defined for $x>4$ , thus the function as a whole is defined for $x>4$ .

Now the function can be written as:

$y=\log[(x-4)(x-3)]-\log(x-4)$

$=\log(x-4)+\log(x-3)-\log(x-4)$

$=\log(x-3)$

We can sketch this graph more easily than the graph of the original function, but the graph is only valid for $x>4$ :

Return to Assignments Logarithmic functions and graphs

Assignments

Solution assignment 07 Logarithmic functions and graphs

Assignment 7

Solution

Contact

Tutor Math, Statistics or GMAT?

Language preference