Terug naar Opgaven Optimaliseren ![]()
Opgave 8
Ga na of de functie:
![]()
een maximum of minimum heeft.
Uitwerking
Natuurlijk is ![]() .
.
Kandidaten voor een maximum of minimum worden gevonden door de afgeleide gelijk aan ![]() te stellen. De afgeleide wordt gevonden met behulp van de quotiëntregel:
te stellen. De afgeleide wordt gevonden met behulp van de quotiëntregel:
![]()
Een breuk is gelijk aan ![]() als zijn teller gelijk is aan
als zijn teller gelijk is aan ![]() dus moeten we oplossen:
dus moeten we oplossen:
![]()
en dus geldt:
![]() of
of ![]()
Wanneer we de tweede afgeleide willen gebruiken om te onderzoeken wanneer er sprake is van een maximum of minimum, moeten we voor het differentiëren van ![]() opnieuw de kettingregel toepassen. Dat vergt enig rekenwerk. Het tekenonderzoek van
opnieuw de kettingregel toepassen. Dat vergt enig rekenwerk. Het tekenonderzoek van ![]() is gemakkelijker. Omdat in de noemer
is gemakkelijker. Omdat in de noemer ![]() staat die altijd positief is, hoeven we alleen naar de teller te kijken. Deze bevat een tweedegraads functie waarvan de grafiek een dalparabool is. Rond het linker snijpunt
staat die altijd positief is, hoeven we alleen naar de teller te kijken. Deze bevat een tweedegraads functie waarvan de grafiek een dalparabool is. Rond het linker snijpunt ![]() gaat de afgeleide van + via 0 naar - en dus is er een maximum voor
gaat de afgeleide van + via 0 naar - en dus is er een maximum voor ![]() . Voor
. Voor ![]() geldt het omgekeerde en daar is dus sprake van een minimum.
geldt het omgekeerde en daar is dus sprake van een minimum.
De optima zijn dus ![]() (maximum) en
(maximum) en ![]() (minimum).
(minimum).
Deze uitkomst lijkt vreemd: de minimale waarde is groter dan de maximale waarde. Schets de grafiek van de functie en merk op dat tussen beide optima een verticale asymptoot ligt.
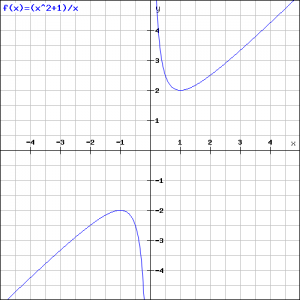
Er is nog een tweede aanpak mogelijk. Alvorens de functie te differentiëren kan hij worden vereenvoudigd door eerst de x uit te delen:
![]()
Van deze functie is het veel gemakkelijker de afgeleide te bepalen.
Terug naar Opgaven Optimaliseren ![]()

