Return to Assignments Optimizing ![]()
Assignment 8
Verify whether the function:
![]()
has a maximum or a minimum.
Solution
Naturally we have ![]() .
.
Candidates for a maximum or a minimum can be found by making the first derivative equal to ![]() and solve the resulting equation. We find the derivative using the quotient rule:
and solve the resulting equation. We find the derivative using the quotient rule:
![]()
A fraction equals ![]() if its numerator equals
if its numerator equals ![]() and thus we have to solve:
and thus we have to solve:
![]()
and thus:
![]() or
or ![]()
In order to investigate whether a point is a maximum or a minimum we could use the second derivative. However this requires a lot of calculations. It is easier to consider the sign of the first derivative. The denominator ![]() is always positive, we only have to look at the numerator. This contains a quadratic function of which the graph is an 'opens up' parabola. Around the left intersection point
is always positive, we only have to look at the numerator. This contains a quadratic function of which the graph is an 'opens up' parabola. Around the left intersection point ![]() the first derivative goes from + via
the first derivative goes from + via ![]() to - and thus there is a maximum for
to - and thus there is a maximum for ![]() . For
. For ![]() the reverse holds and thus we have a minimum for this point.
the reverse holds and thus we have a minimum for this point.
The extremes are thus ![]() (maximum) and
(maximum) and ![]() (minimum).
(minimum).
This result seems strange: a minimum that is greater than a maximum but it is not. Look at the graph below. Notice that the line ![]() is an asymptote.
is an asymptote.
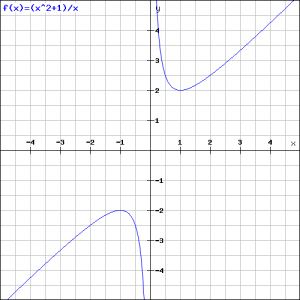
There is also another approach. Before differentiating the function we first simplify it by dividing both numerator and denominator by ![]() .
.
![]()
This function is easier to handle and it immediately shows the existence of the asymptote ![]() .
.
Return to Assignments Optimizing ![]()

