Terug naar Opgaven Gebroken functies en grafieken
Opgave 10
Onderzoek de functie:
![]()
en schets met behulp van de resultaten de grafiek.
Uitwerking
Het lijkt erop dat ![]() een verticale asymptoot is (voor
een verticale asymptoot is (voor ![]() wordt de functie
wordt de functie ![]() . Bij het zoeken naar een horizontale asymptoot ondervinden we enkele problemen. Immers voor
. Bij het zoeken naar een horizontale asymptoot ondervinden we enkele problemen. Immers voor ![]() of
of ![]() nadert de functie ook naar
nadert de functie ook naar ![]() . Om toch wat meer informatie te krijgen over hoe de functie zich gedraagt voor
. Om toch wat meer informatie te krijgen over hoe de functie zich gedraagt voor ![]() of
of ![]() , herschrijven we de functie als volgt:
, herschrijven we de functie als volgt:
![]()
We zien dat de functie nadert tot de functie:
![]()
wanneer ![]() of
of ![]() . In feite fungeert deze parabool als een bijzondere asymptoot.
. In feite fungeert deze parabool als een bijzondere asymptoot.
Het is duidelijk dat de grafiek geen snijpunt met de ![]() -as (
-as (![]() ) heeft. Het snijpunt met de
) heeft. Het snijpunt met de ![]() -as wordt gevonden door de vergelijking:
-as wordt gevonden door de vergelijking:
![]()
op te lossen. We zien onmiddellijk dat ![]() de oplossing en dus kunnen we (door
de oplossing en dus kunnen we (door ![]() te delen door
te delen door ![]() ) schrijven:
) schrijven:
![]()
De tweedegraads functie heeft een discriminant die kleiner dan ![]() is en dus levert die geen oplossingen. Het enige snijpunt met de
is en dus levert die geen oplossingen. Het enige snijpunt met de ![]() -as is dus
-as is dus ![]() .
.
Vanwege het bijzondere karakter van de functie en omdat we opnieuw niet via differentiëren een maximum of minimum willen bepalen, kijken we nog wat nader naar het gedrag van de functie in de buurt van ![]() . We zien dat de tweede term
. We zien dat de tweede term ![]() in de buurt van
in de buurt van ![]() de grootste (positief of negatief) waarde heeft:
de grootste (positief of negatief) waarde heeft:
![]()
en
![]()
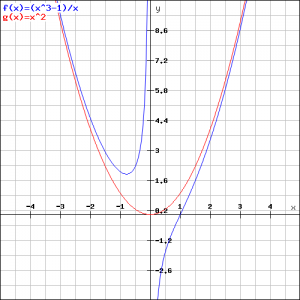
Op grond van dit onderzoek kunnen we de grafiek schetsen. De parabool is ook afgebeeld.
Terug naar Opgaven Gebroken functies en grafieken