Solution assignment 10 Fractional functions and graphs

Return to Assignments Fractional functions and graphs

Assignment 10

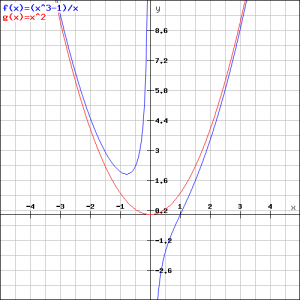
Investigate the function:

$y=\displaystyle\frac{x^3-1}{x}$

and sketch its graph.

Solution

For $x=0$ we have a vertical asymptote (for $x=0$ the function becomes $\pm\infty$ ). When we try to find a horizontal asymptote we encounter some problems, because for $x\to\infty$ or $x\to-\infty$ the graph approaches $\pm\infty$ . In order to get more information of the behavior of the function for $x\to\infty$ or $x\to-\infty$ , we rewrite the function as follows:

$y=\displaystyle\frac{x^3-1}{x}=\displaystyle\frac{x^3}{x}-\displaystyle\frac{1}{x}= x^2-\displaystyle\frac{1}{x}$

We see that the graph approaches:

$y=x^2$

when $x\to\infty$ or $x\to-\infty$ . In fact, this parabola is a special asmptote.
It is clear that the graph has no intersection points with the $Y$ -axis ( $x=0$ ). The intersection point with the $X$ -axis can be found by solving the equation:

$x^3-1=0$

We notice immediately that this equation has the solution $x=1$ and thus we can factorize the function $x^3-1$ :

$x^3-1=(x-1)(x^2+x+1)=0$

The quadratic function has a discriminant which is less than $0$ is and thus has no solutions. Thus the only intersection point with the $X$ -as is $(1,0)$ .
Because of the special nature of the function we look at it in more detail near $x=0$ . We notice that the second term $\displaystyle\frac{1}{x}$ near $x=0$ has either the largest (positive or negative) value: