Terug naar Opgaven Gebroken functies en grafieken
Opgave 7
Bepaal van de functie:
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de 
-as als dat bestaat;
het snijpunt met de 
-as als dat bestaat.
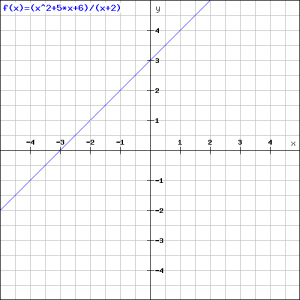
Schets met behulp van deze resultaten de grafiek.
Uitwerking
De lijn 
lijkt een asymptoot te zijn, maar wanneer we deze waarde in de formule invullen krijgen we 
. Dat de teller voor de waarde 
oplevert, betekent dat de teller een factor 
bevat. Inderdaad, de teller blijkt te kunnen worden ontbonden in factoren: 
. Hierdoor kan de functie worden herschreven als:
onder voorwaarde dat 
.
We hoeven nu geen ingewikkelde berekeningen meer uit te voeren. Ook zijn er geen asymptoten meer te bepalen. De grafiek van de functie is die van 
, het punt 
uitgesloten. Wel kunnen we zien dat de grafiek tot 
nadert wanneer 
nadert tot 
. Zie de grafiek die geldt voor .
Terug naar Opgaven Gebroken functies en grafieken
