Return to Assignments Fractional functions and graphs
Assignment 7
Given the function:
![]()
Find:
the vertical asymptote;
the horizontal asymptote;
the intersection point with the ![]() -as if it exists;
-as if it exists;
the intersection point with the ![]() -as if it exists.
-as if it exists.
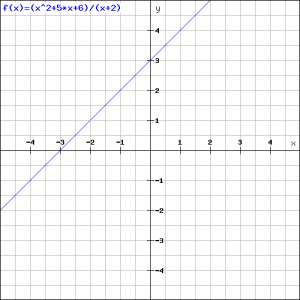
Based on these results sketch the result in the figure.
Solution
The line ![]() seems to be an asymptote. However, when we substitute this value in the formula we get
seems to be an asymptote. However, when we substitute this value in the formula we get ![]() . That the numerator yields
. That the numerator yields ![]() for
for ![]() means that the numerator contains the factor
means that the numerator contains the factor ![]() . Indeed, the numerator can be factorized:
. Indeed, the numerator can be factorized: ![]() . Now the function can be rewritten:
. Now the function can be rewritten:
![]() if
if ![]() .
.
We do not need to do complicated calculations any more. There also no asymptotes. The graph of the function is equal to the graph of ![]() , excluded the point
, excluded the point ![]() . The graph approaches
. The graph approaches ![]() if
if ![]() approaches
approaches ![]() The graph in the figure is valid, exluded the point
The graph in the figure is valid, exluded the point ![]() .
.