Terug naar Opgaven Gebroken functies en grafieken
Opgave 9
Onderzoek de functie:
en schets met behulp van de resultaten de grafiek.
Uitwerking
We zien dat 
een verticale asymptoot is (voor wordt de functie 
. Bij het zoeken naar een horizontale asymptoot ondervinden we enkele problemen. Immers voor 
of 
nadert de functie ook naar 
. Om toch wat meer informatie te krijgen over hoe de functie zich gedraagt voor of 
, herschrijven we de functie als volgt:
We zien dat de functie tot de functie 
nadert wanneer of . In feite heeft de functie een schuine asymptoot .
Verder zien we dat het snijpunt met de 
-as is 
en het snijpunt met de 
-as krijgen we door de vergelijking op te lossen die ontstaat wanneer 
wordt gekozen. We moeten dus de volgende vergelijking oplossen:
Een breuk is gelijk aan 
wanneer de teller gelijk aan is, dus moeten we oplossen:
Dit is een tweedegraads vergelijking. De discriminant van de tweedegraads functie is:
is kleiner dan voor de gegeven coëfficiënten. De vergelijking heeft dus geen oplossingen en dus heeft de grafiek geen snijpunten met de -as.
Met behulp van de differentiaalrekening kunnen we ook nog berekenen of en zo ja voor welke waarde(n) van 
de grafiek een maximum of een minimum heeft, maar die berekening laten we hier achterwege. Wie met differentiëren vertrouwd is, kan ook dit onderdeel nog uitwerken.
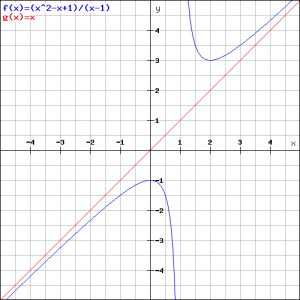
Wij hebben inmiddels genoeg informatie om de grafiek te schetsen. In de figuur zijn zowel de gevraagde grafiek als de rechte lijn getrokken.
Terug naar Opgaven Gebroken functies en grafieken
