Return to Assignments Fractional functions and graphs
Assignment 9
Investigate the function:
![]()
and sketch its graph.
Solution
![]() is a vertical asymptote (for
is a vertical asymptote (for ![]() the function becomes
the function becomes ![]() , but this is not the case as we will see later. When we want to find the horizontal asymptote we encounter some problems. For
, but this is not the case as we will see later. When we want to find the horizontal asymptote we encounter some problems. For ![]() of
of ![]() the function approaches
the function approaches ![]() . In order to get more information of the behavior of the function for
. In order to get more information of the behavior of the function for ![]() of
of ![]() , we rewrite the function as follows:
, we rewrite the function as follows:
![]()
We see that the function approaches ![]() when
when ![]() or
or ![]() . This means that the function approaches the line:
. This means that the function approaches the line: ![]() .
.
We also notice that the intersection point with the ![]() -axis is
-axis is ![]() and we find the intersection point with the
and we find the intersection point with the ![]() -axis by solving the equation which we get by taking
-axis by solving the equation which we get by taking ![]() . So we have to solve the following equation:
. So we have to solve the following equation:
![]()
If a fraction equals ![]() then the numerator equals
then the numerator equals ![]() and thus we have to solve:
and thus we have to solve:
![]()
This is a quadratic equation. The discriminant:
![]()
is less than ![]() . The equation has no solutions and thus the graph has no intersection points with the
. The equation has no solutions and thus the graph has no intersection points with the ![]() -axis.
-axis.
Using calculus we can also calculate by differentiation for which values of ![]() the graph has a maximum or minimum, but we do not do this here. If you know enough of differentiation, please do this yourself.
the graph has a maximum or minimum, but we do not do this here. If you know enough of differentiation, please do this yourself.
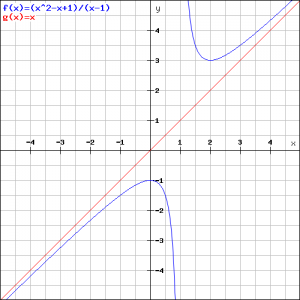
We have enough information to sketch the graph. In the figure both the graph and the line ![]() are depicted.
are depicted.