Terug naar Opgaven Gebroken functies en grafieken
Opgave 6
Bepaal van de functie:
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de 
-as als dat bestaat;
het snijpunt met de 
-as als dat bestaat.
Schets met behulp van deze resultaten de grafiek.
Uitwerking
Deze functie ziet er iets anders uit dan we gewend zijn, maar na enkele berekeningen komen we toch weer op bekend terrein. We herschrijven:
Deze functie heeft de bekende vorm.
De verticale asymptoot van deze functie is 
, de waarde waarvoor de noemer 
wordt. De horizontale asymptoot vinden we door te onderzoeken tot welke lijn de grafiek nadert wanneer 
of 
en dat is 
, dus de -as. Verder zien we dat we voor het snijpunt met de -as (kies 
) krijgen 
. Er is geen snijpunt met de -as omdat de -as asymptoot is.
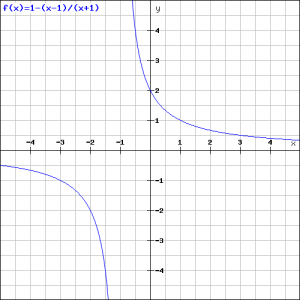
De grafiek ziet er dan als volgt uit.
Terug naar Opgaven Gebroken functies en grafieken
