Return to Assignments Fractional functions and graphs
Assignment 6
Given the function:
Find:
the vertical asymptote;
the horizontal asymptote;
the intersection point with the 
-as if it exists;
the intersection point with the 
-as if it exists.
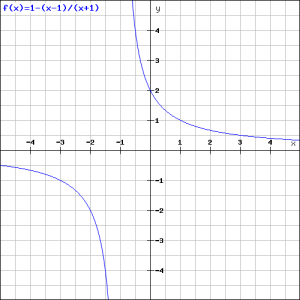
Based on these results sketch the result in the figure.
Solution
This function looks slightly different than we are used to, but after a few calculations we come on familiar ground.
We rewrite:
Now this function has the familiar form.
The vertical asymptote of this function is 
, i.e. the value for which the denominator equals 
. We find the horizontal asymptote by trying to find the value of 
if 
or 
and that is 
, thus the -axis. Furthermore we notice that the intersection point with the -axis (take 
) is 
. There is no intersection point with the -axis because the -axis is an asymptote.
The graph is depicted in the following figure.
