Uitwerking opgave 09 Exponentiële functies en grafieken

Terug naar Opgaven Exponentiële functies en grafieken

Opgave 9

Teken de grafieken van de functies:

$f: y=3^x$

$g: y=(\displaystyle\frac{1}{3})^{x-1}+2$

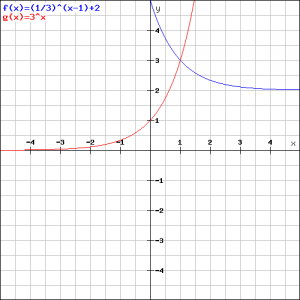
Bereken vervolgens het snijpunt van beide grafieken.

Uitwerking

Hoe de grafieken van beide functies kan worden getekend, is in eerdere opgaven al behandeld.
Om het snijpunt van beide grafieken te vinden, moeten we de volgende vergelijking oplossen:

$3^x=(\displaystyle\frac{1}{3})^{x-1}+2$

$3^x=(3^{-1})^{x-1}+2$

$3^x=3^{-x+1}+2$

We vermenigvuldigen beide leden met $3^x$ en krijgen dan:

$3^{2x}-2.3^x-3=0$

We stellen van deze vergelijking de schaduwvergelijking op door te kiezen:

$y=3^x$

We krijgen dan:

$y^2-2y-3=0$

$(y-3)(y+1)=0$

We hebben de tweedegraads vergelijking ontbonden in factoren. De oplossingen van deze vergelijking zijn dus: $y=3$ of $y=-1$ . De laatste voldoet niet omdat $y$ een exponentiële functie is en dus positief. De oplossing wordt daarom gevonden uit: