Terug naar Opgaven Optimaliseren 
Opgave 10
Vind het optimum van de functie:
zonder gebruik te maken van het tekenverloop van de eerste afgeleide of de tweede afgeleide.
Uitwerking
Om de kandidaten voor een optimum te vinden, moeten we de afgeleide van de functie gelijk aan 
stellen:
dus:
en deze vergelijking heeft als oplossing:
of 
Nadere bestudering van de derdegraads functie leert dat de functie van linksonder (derde kwadrant) naar rechtsboven (eerste kwadrant) loopt. Immers, wanneer 
erg groot en negatief is, zorgt 
ervoor dat ook de 
negatief zal zijn. Omgekeerd, wanneer x erg groot en positief is, zal de y ook positief zijn.
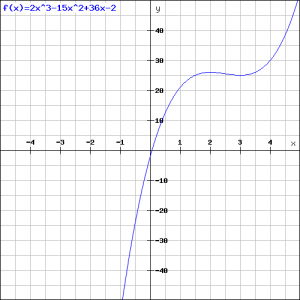
Om deze reden zal de grafiek in het punt met een maximum zijn en in het punt met een minimum, zie figuur.
Terug naar Opgaven Optimaliseren
