Terug naar Opgaven Gebroken functies en grafieken
Opgave 5
Bepaal van de functie:
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de 
-as als dat bestaat;
het snijpunt met de 
-as als dat bestaat.
Schets met behulp van deze resultaten de grafiek.
Uitwerking
Deze functie ziet er iets anders uit dan we gewend zijn, maar toch kunnen we ongeveer dezelfde methoden gebruiken om de antwoorden op de vragen te vinden.
De verticale asymptoot van deze functie is 
, de waarde waarvoor de noemer 
wordt. De horizontale asymptoot vinden we door te onderzoeken tot welke lijn de grafiek nadert wanneer 
of 
en dat is 
. Dit kunnen we op twee manieren berekenen.
We herschrijven de functie als volgt:
Wanneer of nadert de tweede term tot en dus nadert 
tot 
. (Merk op dat de oorspronkelijke functie dus wel degelijk de vorm kan aannemen die we gewend waren.)
De tweede manier is als volgt: deel teller en noemer door de hoogste macht van 
, in dit geval is dat , en neem vervolgens de limiet.
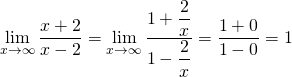
Deze aanpak kunnen we ook gebruiken voor .
Verder zien we dat we voor het snijpunt met de -as (kies 
) krijgen 
. Het snijpunt met de -as krijgen we door 
te kiezen en vervolgens de vergelijking op te lossen. We vinden dan 
.
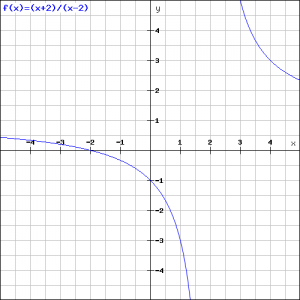
De grafiek ziet er dan als volgt uit.
Terug naar Opgaven Gebroken functies en grafieken
