Terug naar Opgaven Gebroken functies en grafieken
Opgave 2
Bepaal van de functie:
de verticale asymptoot;
de horizontale asymptoot;
het snijpunt met de 
-as als dat bestaat;
het snijpunt met de 
-as als dat bestaat.
Schets met behulp van deze resultaten de grafiek.
Uitwerking
Dit is nog steeds een eenvoudige gebroken functie. De verticale asymptoot is 
. De horizontale asymptoot vinden we door te onderzoeken tot welke lijn de grafiek nadert wanneer 
of 
en dat is 
. De grafiek snijdt de -as bij 
. De grafiek heeft geen snijpunt met de -as, want de -as is een asymptoot. Dit resultaat kan ook worden verkregen door de vergelijking op te lossen met : deze vergelijking heeft geen oplossing.
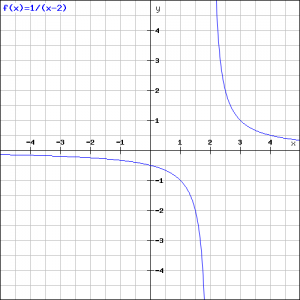
De grafiek ziet er daarom als volgt uit:
Terug naar Opgaven Gebroken functies en grafieken
