Return to Assignments Fractional functions and graphs
Assignment 10
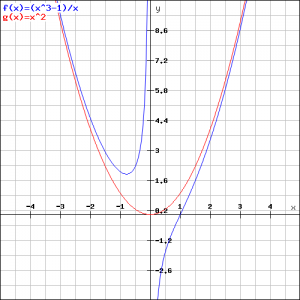
Investigate the function:
![]()
and sketch its graph.
Solution
For ![]() we have a vertical asymptote (for
we have a vertical asymptote (for ![]() the function becomes
the function becomes ![]() ). When we try to find a horizontal asymptote we encounter some problems, because for
). When we try to find a horizontal asymptote we encounter some problems, because for ![]() or
or ![]() the graph approaches
the graph approaches ![]() . In order to get more information of the behavior of the function for
. In order to get more information of the behavior of the function for ![]() or
or ![]() , we rewrite the function as follows:
, we rewrite the function as follows:
![]()
We see that the graph approaches:
![]()
when ![]() or
or ![]() . In fact, this parabola is a special asmptote.
. In fact, this parabola is a special asmptote.
It is clear that the graph has no intersection points with the ![]() -axis (
-axis (![]() ). The intersection point with the
). The intersection point with the ![]() -axis can be found by solving the equation:
-axis can be found by solving the equation:
![]()
We notice immediately that this equation has the solution ![]() and thus we can factorize the function
and thus we can factorize the function ![]() :
:
![]()
The quadratic function has a discriminant which is less than ![]() is and thus has no solutions. Thus the only intersection point with the
is and thus has no solutions. Thus the only intersection point with the ![]() -as is
-as is ![]() .
.
Because of the special nature of the function we look at it in more detail near ![]() . We notice that the second term
. We notice that the second term ![]() near
near ![]() has either the largest (positive or negative) value:
has either the largest (positive or negative) value:
![]()
and
![]()
Based on this investigation we can sketch the graph. We also depicted the parabola.