Return to Assignments Fractional functions and graphs
Assignment 2
Given the function:
![]()
Find:
the vertical asymptote;
the horizontal asymptote;
the intersection point with the ![]() -as if it exists;
-as if it exists;
the intersection point with the ![]() -as if it exists.
-as if it exists.
Based on these results sketch the result in the figure.
Solution
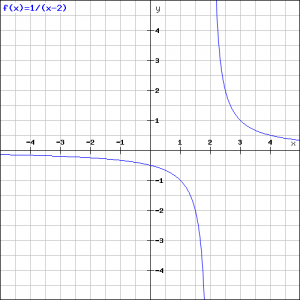
This is still a quite simple fractional function. The vertical asymptote is ![]() . We find the horizontal asymptote by investigating the line to which the graph approaches if
. We find the horizontal asymptote by investigating the line to which the graph approaches if ![]() and that is
and that is ![]() . The graph intersects the
. The graph intersects the ![]() -axis at
-axis at ![]() . The graph has no intersection point with the
. The graph has no intersection point with the ![]() -axis, because the
-axis, because the ![]() -axis is an asymptote. This result can also be obtained by solving the equation with
-axis is an asymptote. This result can also be obtained by solving the equation with ![]() : this equation has no solution.
: this equation has no solution.
The graph is depicted in the following figure.