Terug naar Opgaven Tweedegraads functies en grafieken
Opgave 3
Gegeven de functie:
![]()
Beantwoord de volgende vragen:
- Wat is het snijpunt van de grafiek met de
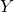 -as;
-as; - Heeft deze grafiek snijpunten met de
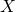 -as, en zo ja, hoeveel en bepaal de coördinaten.
-as, en zo ja, hoeveel en bepaal de coördinaten. - Bepaal de symmetrie-as.
Uitwerking
1. Omdat de ![]() in de formule gelijk is aan
in de formule gelijk is aan ![]() , is het snijpunt met de
, is het snijpunt met de ![]() -as gelijk aan
-as gelijk aan ![]() .
.
2. Om na te gaan of de grafiek van de functie snijpunten heeft met de ![]() -as, moet de discriminant worden berekend. We kunnen ook constateren dat de vergelijking kan worden ontbonden in factoren:
-as, moet de discriminant worden berekend. We kunnen ook constateren dat de vergelijking kan worden ontbonden in factoren:
![]()
Daarmee slaan we twee vliegen in een klap. Er zijn twee snijpunten met de ![]() -as en hun coördinaten zijn
-as en hun coördinaten zijn ![]() en
en ![]() .
.
3. De symmetrie-as ligt daar precies in het midden tussen, dus de symmetrie-as is ![]() .
.
Terug naar Opgaven Tweedegraads functies en grafieken

