Return to Assignments Fractional functions and graphs
Assignment 5
Given the function:
Find:
the vertical asymptote;
the horizontal asymptote;
the intersection point with the 
-as if it exists;
the intersection point with the 
-as if it exists.
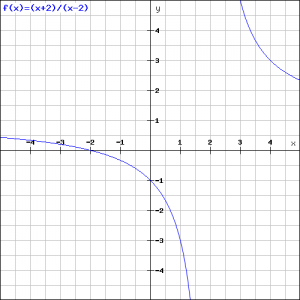
Based on these results sketch the result in the figure.
Solution
This function looks slightly different than we are used to, but we can use similar methods to find the answers to the questions.
The vertical asymptote of this function is 
, i.e. the value for which the denominator equals 
. We find the horizontal asymptote by finding the line to which the graph approaches when 
or 
and that is 
. We can calculate this in two ways.
For the first method we rewrite the function as follows:
When or the second term approaches and thus 
approaches 
.
The second way is as follows: divide numerator and denominator by the highest power of 
, in this case that is . Next take the limit.
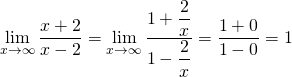
We can also use this approach for .
We also notice that the intersection point with the -axis (take 
) is 
. The intersection point with the -axis can be found by substituting 
and solving the equation. We calculate 
.
The graph is depicted in the figure.
