Terug naar Opgaven Absolute waarde |x|
Opgave 6
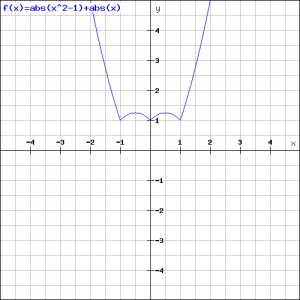
Teken de grafiek van 
Uitwerking
We gebruiken de definitie van de absolute waarde.
Voor beide absolute waarden passen we de definitie toe.
als 
, dus als 
of 
(zie ook opgave 4). We noemen dit interval A.
als 
. We noemen dit interval B.
als 
. We noemen dit interval C.
als 
. We noemen dit interval D.
Voor het tekenen van de grafiek onderscheiden we de volgende intervallen.
, dit is de doorsnede van de intervallen A en D, kortweg AD.
, dit is de doorsnede van de intervallen B en D, kortweg BD.
, dit is de doorsnede van de intervallen B en C, kortweg BC.
, dit is de doorsnede van de intervallen A en C, kortweg AC.
Voor AD geldt: 
Voor BD geldt: 
Voor BC geldt: 
Voor AC geldt: 
Het resultaat zijn gedeelten van een viertal verschillende parabolen. De eerste gaat bijvoorbeeld door 
en heeft een minimum voor 
. Bereken dezelfde kenmerken voor de andere parabolen en schets op grond hiervan de grafiek. Constateer dat de grafiek bij de gegeven functie past.
Terug naar Opgaven Absolute waarde |x|
