Optimizing f(x)

Summary and examples

$f'(a)$ is the derivative of a function $f(x)$ in a point $(a,f(a))$ and is the slope of the tangent line at that point of the graph of that function.

When $f'(a)=0$ it means that the tangent line in $(a, f(a))$ has a slope $0$ and thus that it is horizontal to the $X$ -axis. For such a point there are three possibilities:

the point is a (local) maximum;
the point is a (local) minimum;
the point is a horizontal inflection point (an example is the graph of $y=x^3$ ).

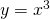When we want to know in which points a function $f(x)$ has a local maximum, minimum or horizontal inflection point, we calculate the derivative $f'(x)$ and try to find for which values $f'(x)=0$ , for these values of $x$ the derivative equals zero and the tangent line is horizontal.

Example 1

Determine the minimum of the parabola:

$y=2x^2-8x-4$

We already know that this parabola 'opens up' (the coefficient of the square equals $2$ and thus $\geq0$ ) and thus has a minimum that lies on the symmetry-axis, see Quadratic functions and graphs.

We differentiate the function and get:

$y'=4x-8=0$

and thus:

$x=2$

The parabola has a minimum in the point $(2,-12)$ .

Example 2

Quadratic functions (the graphs are parabolas):

$y=ax^2+bx+x, (a\neq0)$

have a maximum or minimum that lies on the symmetry-axis:

$x_{top}=-\displaystyle\frac{b}{2a}$

We can also calculate this by differentiation. The derivative of the function above is:

$y'=2ax+b$

The derivative is equal to $0$ when:

$x=-\displaystyle\frac{b}{2a}$

which is the $x$ -coordinate of the top.

The values of $x$ for which the derivative of the function equals $0$ are candidates for a maximum, minimum or horizontal inflection point, but we do not know yet which of the three is the case. This requires further investigation. There are two different methods for this.

Method 1: consider the sign of the first derivative

The derivative of a maximum in a point $x=a$ is equal to $0$ .
Left to the maximum the function is increasing and thus $f'(x)>0$ for $x<a$ .
Right to the maximum the function is decreasing and thus $f'(x)<0$ for $x>a$ .
So the sign of the first derivative $f'(x)$ around the maximum $x=a$ has the following signs:

maximum : + $0$ -.

Similarly, the sign of the first derivative $f'(x)$ around the minimum $x=a$ has the following signs:

minimum: - $0$ +.

For a horizontal inflection point we find similarly:

horizontal inflection point : + $0$ + or - $0$ -.

Method 2: consider the 2nd derivative

When $x=a$ is one of the solutions of the equation $f'(x)=0$ it is a candidate for a maximum, minimum or horizontal inflection point. Then the following holds.
If:

$f''(a) > 0$ , then $x=a$ is a minimum;

$f''(a) < 0$ , then $x=a$ is a maximum;

$f''(a) = 0$ , then $x=a$ is a horizontal inflection point.

Example 3

Check whether the function:

$y=\displaystyle\frac{1}{3}x^3-x+1$

has a maximum and/or a minimum.

The derivative is:

$y'=x^2-1$

The derivative equals $0$ if:

$x^2-1=0$

so if:

$x=1$ or $x=-1$

The corresponding points on the graph are, respectively:

$(1,\displaystyle\frac{1}{3})$ or $(-1,-\displaystyle\frac{5}{3})$

Now we check both methods.

Method 1

Around $x=-1$ we find the following signs of $f'x)$ :

+ $0$ - and thus there is a maximum.

Around $x=1$ we find the following signs of $f'x)$ :

- $0$ + and thus there is a minimum.

Method 2

We have to calculate the second derivative:

$y''=2x$

Then:

$y''(-1)=-2<0$ and thus the function has a maximum for $x=-1$

and

$y''(1)=2>0$ and thus the function has a minimum for $x=1$

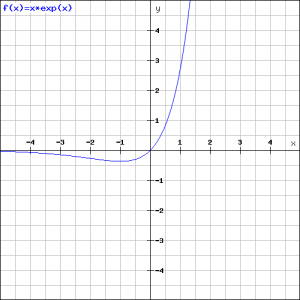
Example 4

Check whether the function:

$y=xe^x$

has a local maximum or minimum.

The derivative of the function is, using the product rule:

$y'=1\cdot{e^x}+xe^x=(x+1)e^x$

The derivative is $0$ when $x = -1$ and thus the point $(-1, e^{-1})$ is a candidate for either a maximum or minimum. Further research should reveal which of the two it is. It is even possible that it is a point of inflection.
We can use either method, but the second method is more laborious because then we need to use the production rule again. Therefore we take method 1 and only need to consider the sign of $x+1$ because the exponential function $e^x$ is always positive.