Logarithmic functions and graphs

Summary and examples

The logarithmic and the exponential function are each other's inverses. In the Netherlands it is customary to write the logarithmic function as follows:

$y= ^g\log(x)$

i.e. the so-called base $g$ is written upper left. Elsewhere, particularly in Anglo-American countries, the logarithm is written as:

$y=\log_b(x)$

where $b$ stands for base. We will be using the latter expression. Often, the $log$ is written without parentheses around the argument. We choose to use parentheses to avoid confusion.

Thus the logarithmic function is:

$y=\log_b(x)$

under the following conditions:

$b>0$ en $b\neq1$

$x>0$

In order to understand these conditions we use the definition of the logarithm:

$y=\log_b(x)\Longleftrightarrow x=b^x$

By using this formula we can quickly calculate logarithms.

Example 1

Calculate:

$\log_{10}(100)$

According to the above definition we can write:

$y=\log_{10}(100)\Longleftrightarrow 100=10^y$

and we see immediately that $y=2$ is a solution.

Example 2

Calculate:

$\log_3(27)$

According to the above definition we can write:

$y=\log_3(27)\Longleftrightarrow 27=3^y$

and see immediately that $y=3$ is a solution.

Example 3

Calculate:

$\log_4(\displaystyle\frac{1}{64})$

According to the above definition we can write:

$\displaystyle\frac{1}{64}=4^y$

We rewrite:

$4^y=\displaystyle\frac{1}{64}=\displaystyle\frac{1}{4^3}=4^{-3}$

and thus the solution is $y=-3$ .

Example 4

Calculate:

$\log_\frac{1}{2}(16)$

According to the above definition we can write:

$y=\log_\frac{1}{2}(16)\Longleftrightarrow 16=(\frac{1}{2})^y=(2^{-1})^y=2^{-y}$

So:

$2^{-y}=16=2^4$

and thus the solution is:

$y=-4$

We have two remarks about the base $b$ .

When we do not give a base, then we mean 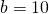$b=10$ ; then we write $\log(x)$ .
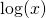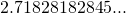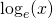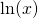When the base is meant to be $e$ (Euler's number, $2.71828182845...$ ), then we write $\log_e(x)$ as $\ln(x)$ . Such a logarithm is called a natural logarithm (logarithm naturalis).

There are four formulas that are commonly used when working with logarithms. It is useful to have them always on hand so that you do not always need to grab a book.
These are the formulas:

$\log_b(xy)=\log_b(x)+\log_b(y)$
$\log_b(\displaystyle\frac{x}{y})=\log_b(x)-\log_b(y)$
$\log_b(x^n)=n\log_b(x)$
$\log_b(x)=\displaystyle\frac{\log_c(x)}{\log_c(b)}$

For $c$ the same conditions hold as for $b$ . On these formulas we have to make some comments. They do not just fall out of the air, but can be derived using the definition. We also see that the third formula follows directly from the first. The last formula applies to every $c$ meeting the aforementioned requirements for the base. The usefulness of this formula is great, so will confirm each user of a calculator. When someone wants to use a calculator to calculate:

$\log_5(7)$

he would have to search for the key that can be used for the log base $5$ . However, he will find the $\log$ -key (base $10$ ) and the $\ln$ -key (base $e$ ), but not a key for the log with base $5$ . Using the fourth formula, he will be able to calculate the answer:

$\log_5(7)=\displaystyle\frac{\log(7)}{\log(5)}\approx1.21$

Example 5

Solve:

$\ln(x^2)+3\ln(x)=10$

Using the third formula we write:

$2\ln(x)+3\ln(x)=10$

$5\ln(x)=10$

$\ln(x)=2$

$x=e^2$

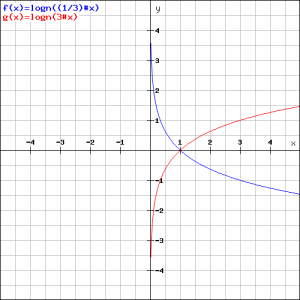
The graph of the logarithmic function:

$y=\log_b(x)$

depends on the base $b$ . In the figure below we see the graphs of:

$l_1: y=\log_3(x)$

$l_2: y=\log_\frac{1}{3}(x)$

The blue graph corresponds to $l_1$ , the red to $l_2$ . Using the definition shows that $l_1$ en $l_2$ are each other's mirrors in the $X$ -axis.
Both graphs go through the point $(1,0),$ which is the case for all admitted bases.