Solution assignment 05 Improper integrals

Return to Assignments Improper integrals

Assignment 5

Calculate:

$\displaystyle\int_{0}^{\infty}{e^{-x}\sin(x)}dx$

Solution

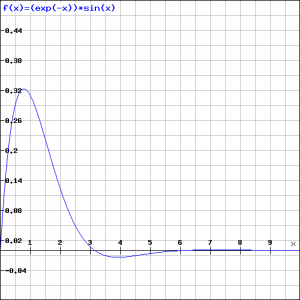
It is clear that this integral converges, because the function $|xe^{-x}|$ is greater than $|e^{-x}\sin(x)|$ from some value of $x$ . The integral of the first function yields a finite result (converges) and this will be the case with the second function. See the graph of $e^{-x}\sin(x)$ in the figure.

The integral has a finite value.

We first look at the calculation of the indefinite integral and use integration by parts:

$\displaystyle\int{e^{-x}\sin(x)}dx=\int{-\sin(x)d(e^{-x})}=$

$=-\sin(x)e^{-x}+\displaystyle\int{e^{-x}}d(\sin(x))=$

$=-\sin(x)e^{-x}+\displaystyle\int{e^{-x}\cos(x)}dx$

It seems that this has not helped us a lot, but by applying integration by parts again we get the following result:

$\displaystyle\int{e^{-x}\sin(x)}dx=-\frac{1}{2}e^{-x}(\sin(x)+\cos(x))+C$

Verify this result by differentiation.

Now we get:

$\displaystyle\int_{0}^{\infty}{e^{-x}\sin(x)}dx=\lim_{a\to\infty}[-\frac{1}{2}e^{-x}(\sin(x)+\cos(x)]_{0}^{a}=\frac{1}{2}$

Return to Assignments Improper integrals

0

Web Design Bangladesh Web Design Bangladesh Mymensingh