Improper integrals

Summary and examples

Improper integrals have an infinite integration interval or an integrand that is infinite within the integration interval.

Examples of these types of integrals are:

$\displaystyle\int_{0}^{\infty}{e^{-x}}dx$ (upper boundary is infinite)

$\displaystyle\int_{0}^{5}{\displaystyle\frac{1}{\sqrt{x}}}dx$ (the integrand is not bounded on the integration-interval (in $x=0)$ .

In spite of the complications of the notion 'infinite' above integrals appear to have a finite value, that is to say an 'infinite' boundary does not lead to an infinite result. We say that such an integral converges. As we will see below, the first integral has the value $1$ and the second integral calculation has the value $2\sqrt{5}$ .
It is not sure that an improper integral gives a finite value. Then we say that the integral diverges. That is the case with the following integral:

$\displaystyle\int_{0}^{\infty}{\displaystyle\frac{1}{\sqrt{x}}}dx$

In order to calculate an improper integral with, for example, an upper boundary $\infty$ , we use the formula:

$\displaystyle\int_{0}^{\infty}{f(x)}dx=\lim_{b\to\infty}\displaystyle\int_{a}^{b}{f(x)}dx$

When we want to calculate an integral of the form:

$\displaystyle\int_{0}^{a}{f(x)}dx$

and, for example, $f(0)$ is not defined, such as with:

$\displaystyle\frac{1}{\sqrt{x}}$

then we use the formula:

$\displaystyle\lim_{a\to 0}\displaystyle\int_{a}^{b}{f(x)}dx$

Example 1

$\displaystyle\int_{0}^{\infty}{e^{-x}}dx=\lim_{a\to\infty}\int_{0}^{a}{e^{-x}}dx=$

$\displaystyle\lim_{a\to\infty}[-e^{-x}]_{0}^{a}=\displaystyle\lim_{a\to\infty}[1-e^{-a}]=1$

Example 2

$\displaystyle\int_{0}^{5}{\frac{1}{\sqrt{x}}}dx=\displaystyle\lim_{a\to0}\int_{a}^{5}{\frac{1}{\sqrt{x}}}dx=$

$=\displaystyle\lim_{a\to0}[2\sqrt{x}]_{a}^{5}=2\sqrt{5}$

For some improper integrals there are techniques to determine whether or not an integral converges or diverges. Such techniques are known as convergence tests. As an example we can mention the following test:

Suppose that $f(x)$ and $g(x)$ are continuous for all $x\geq{a}$ and that holds $|f(x)|\leq{g(x)}$ , for all $x\geq{a}$ .

Then, if $\displaystyle\int_{a}^{\infty}{g(x)}dx$ converges, then also $\displaystyle\int_{a}^{\infty}{f(x)}dx$ .

Furthermore we have: $\displaystyle\int_{a}^{\infty}{f(x)}dx|\leq{\int_{a}^{\infty}{g(x)}dx}$

For more theory about this subject see the literature, for example: Sydsaeter K. and Hammond P., Essential Mathematics for Economic Analysis 3rd ed, and Stewart J.S., Calculus, Concepts and Contexts, 2nd ed.

Example 3

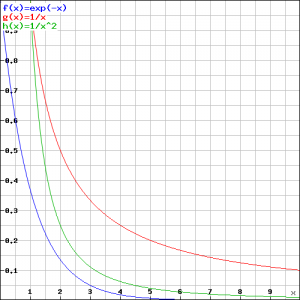
Usually at first sight it is difficult to determine whether an improper integral does or does not converge. For example, on the interval $[1,\infty]$ consider the graphs of the following functions:

$f(x)=e^{-x}$

$g(x)=\displaystyle\frac{1}{x}$

$h(x)=\displaystyle\frac{1}{x^2}$

The question is: which of the three improper integrals converges or diverges?
From the graph we may conclude that if $g(x)$ (red) converges, the other will converge as well. We can also see that $g(x)$ will diverge if $h(x)$ (green) diverges.
Calculations give the following results.