Solution assignment 10 Exponential functions and graphs

Return to Assignments Exponential functions and graphs

Assignment 10

For which value(s) of $p$ do the graphs of the functions:

$f: y=2^x$

$g: y=-(\displaystyle\frac{1}{2})^x+p$

have only one point in common.

Solution

In order to calculate the intersection points of $f$ and $g$ we have to solve the following equation:

$2^x=-(\displaystyle\frac{1}{2})^x+p$

$2^x=-2^{-x}+p$

$2^{2x}=-1+p2^x$

$2^{2x}-p2^x+1=0$

Substituting:

$z=2^x$

in the equation we get:

$z^2-pz+1=0$

This quadratic equation has two coinciding solutions if the discriminant $D=0$ , so if:

$D=p^2-4=0$

$p=2$ or $p=-2$

If $p=-2$ we get $z=-1$ , i.e. $2^x=-1$ and this does not give a solution. Thus the value of $p$ for which both graphs have just one common point is $p=2$ .

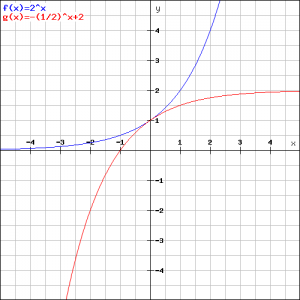
Verify that the common point is $(0,1)$ , see the figure.

Return to Assignments Exponential functions and graphs

0

Web Design Bangladesh Web Design Bangladesh Mymensingh