Solution assignment 10 Optimizing f(x)

Find the extreme of the function:

$y=2x^3-15x^2+36x-2$

without using the sign of the first derivative or the second derivative.

In order to find candidates for extremes we have to differentiate the function and make it equal to $0$ :

$y'=6x^2-30x+36=0$

thus:

$x^2-5x+6=0$

This equation has the solutions:

$x=2$ or $x=3$

A closer look at the cubic equation shows that its graph goes from left under to upper right.

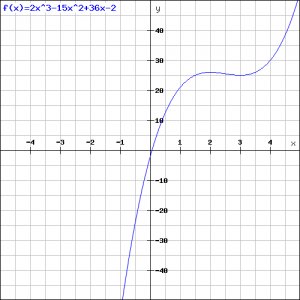
For this reason the graph will have a minimum for $x=2$ and a maximum for $x=3$ , see the figure.