Browse: Home   /   Improper integrals   /   Assignments   /   Solution assignment 04 Improper integrals

Solution assignment 04 Improper integrals

Return to Assignments Improper integrals

Assignment 4

Calculate:

\displaystyle\int_{0}^{\infty}{xe^{-x}}dx

Solution

The integrand is the product of the increasing function x and the (strongly) decreasing function e^{-x}. It may be clear that the decreasing function will win, but it is not clear whether this will be enough to have the integral converge, see the figure.

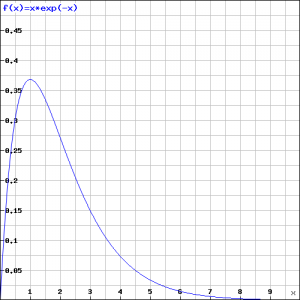
x.exp(-x)

\displaystyle\int_{0}^{\infty}{xe^{-x}}dx=\lim_{a\to\infty}\int_{0}^{a}{xe^{-x}}dx

The primitive of xe^{-x} is -(x+1)e^{-x}

and thus:

\int_{0}^{a}{xe^{-x}}dx=1-(a+1)e^{-a}

After some calculations we get:

1-\displaystyle\lim_{a\to\infty}\frac{a+1}{e^a}=1-0=1

Return to Assignments Improper integrals

0
Web Design BangladeshWeb Design BangladeshMymensingh