Blader: Home   /   Oneigenlijke integralen   /   Opgaven   /   Uitwerking opgave 04 Oneigenlijke integralen

Uitwerking opgave 04 Oneigenlijke integralen

Terug naar Opgaven Oneigenlijke integralen

Bereken:

\displaystyle\int_{0}^{\infty}{xe^{-x}}dx

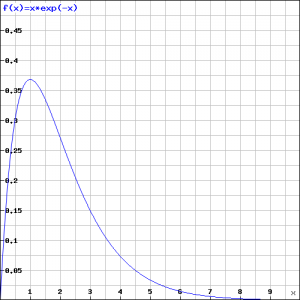
De integrand is het product van een stijgende functie x en een (sterk) dalende functie e^{-x}. Het is duidelijk dat de dalende functie wint, maar of dat genoeg is om de integraal niet oneindig te laten worden, kunnen we berekenen, zie de figuur.

x.exp(-x)

\displaystyle\int_{0}^{\infty}{xe^{-x}}dx=\lim_{a\to\infty}\int_{0}^{a}{xe^{-x}}dx

De primitieve van xe^{-x} is -(x+1)e^{-x} en dus geldt:

\int_{0}^{a}{xe^{-x}}dx=1-(a+1)e^{-a}

De limiet wordt na enig rekenwerk:

1-\displaystyle\lim_{a\to\infty}\frac{a+1}{e^a}=1-0=1

Terug naar Opgaven Oneigenlijke integralen

0
Web Design BangladeshWeb Design BangladeshMymensingh