Terug naar Opgaven Oneigenlijke integralen
Bereken:
![]()
Van deze integraal kunnen we meteen al vaststellen dat hij convergeert. Immers de functie ![]() is groter dan
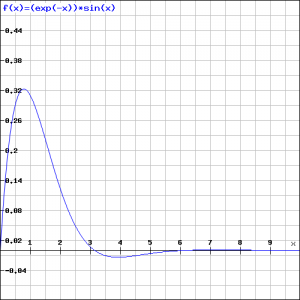
is groter dan ![]() vanaf een zekere waarde. De eerste functie leverde een eindige waarde op en dat zal dus ook het geval zijn met de tweede functie. Zie de grafiek van
vanaf een zekere waarde. De eerste functie leverde een eindige waarde op en dat zal dus ook het geval zijn met de tweede functie. Zie de grafiek van ![]() hieronder.
hieronder.
De integraal heeft dus een 'eindige' waarde.
We kijken eerst naar de berekening van de onbepaalde integraal en maken hierbij gebruik van partieel integreren en krijgen:
![]()
![]()
![]()
Het lijkt erop dat we met deze aanpak niets opschieten, maar door de nieuwe integraal ![]() opnieuw partieel te integreren, krijgen we het volgende resultaat:
opnieuw partieel te integreren, krijgen we het volgende resultaat:
![]()
Controleer dit resultaat door het te differentiëren; dit zou moeten leiden tot de functie ![]() .
.
We krijgen nu:
![]()
Terug naar Opgaven Oneigenlijke integralen