Oneigenlijke integralen

Samenvatting en voorbeelden

Oneigenlijke integralen (in het Engels: improper integrals) zijn integralen waarbij het integratie-interval ‘oneindig’ is (aangegeven door het symbool $\infty$ ), of wanneer de integrand van de integraal binnen het integratie-interval onbegrensd is (‘oneindig wordt').
Voorbeelden van deze integralen zijn:

$\displaystyle\int_{0}^{\infty}{e^{-x}}dx$ (bovengrens is oneindig)

$\displaystyle\int_{0}^{5}{\displaystyle\frac{1}{\sqrt{x}}}dx$ (de integrand is niet begrensd op integratie-interval (in $x=0$ )

Ondanks de complicaties over ‘oneindig’ blijken bovenstaande integralen toch een eindige waarde te hebben, dat wil zeggen dat een grens ‘oneindig’ niet tot een oneindig resultaat leidt. We zeggen dat zulke integralen convergeren. Zoals we hierna zullen zien, heeft de eerste integraal de waarde 1 en bij de tweede integraal leidt een berekening tot het antwoord $2\sqrt{5}$ .
Lang niet altijd levert een oneigenlijke integraal een eindige waarde op. In zulke gevallen zeggen we dat die integraal divergeert. Dat is het geval bij de volgende integraal:

$\displaystyle\int_{0}^{\infty}{\displaystyle\frac{1}{\sqrt{x}}}dx$

Om een oneigenlijke integraal uit te rekenen met bijvoorbeeld een bovengrens $\infty$ , gebruiken we de formule:

$\displaystyle\int_{0}^{\infty}{f(x)}dx=\lim_{b\to\infty}\displaystyle\int_{a}^{b}{f(x)}dx$

Wanneer we een integraal van de vorm:

$\displaystyle\int_{0}^{a}{f(x)}dx$

moeten uitrekenen als bijvoorbeeld $f(0)$ niet is gedefinieerd zoals bij $\displaystyle\frac{1}{\sqrt{x}}$ , gebruiken we de formule:

$\displaystyle\lim_{a\to 0}\displaystyle\int_{a}^{b}{f(x)}dx$

Voorbeeld 1

$\displaystyle\int_{0}^{\infty}{e^{-x}}dx=\lim_{a\to\infty}\int_{0}^{a}{e^{-x}}dx=$

$\displaystyle\lim_{a\to\infty}[-e^{-x}]_{0}^{a}=\displaystyle\lim_{a\to\infty}[1-e^{-a}]=1$

Voorbeeld 2

$\displaystyle\int_{0}^{5}{\frac{1}{\sqrt{x}}}dx=\displaystyle\lim_{a\to0}\int_{a}^{5}{\frac{1}{\sqrt{x}}}dx=$

$=\displaystyle\lim_{a\to0}[2\sqrt{x}]_{a}^{5}=2\sqrt{5}$

Bij sommige oneigenlijke integralen zijn er technieken om te bepalen of een integraal convergeert of divergeert. Zulke technieken staan bekend als convergentietests. Als voorbeeld hiervan kunnen we de volgende test noemen:

Stel dat $f(x)$ en $g(x)$ continu zijn voor alle $x\geq{a}$ en dat geldt: $|f(x)|\leq{g(x)}$ , voor alle $x\geq{a}$ .
Dan, als $\displaystyle\int_{a}^{\infty}{g(x)}dx$ convergeert, dan convergeert tevens: $\displaystyle\int_{a}^{\infty}{f(x)}dx$ .
Verder geldt: $\displaystyle|\int_{a}^{\infty}{f(x)}dx|\leq{\int_{a}^{\infty}{g(x)}dx}$

Voor meer theorie over dit onderwerp wordt verwezen naar diverse wiskundeboeken, bijvoorbeeld Sydsaeter K. en Hammond P., Essential Mathematics for Economic Analysis 3rd ed, en Stewart J.S., Calculus, Concepts and Contexts, 2nd ed.

Voorbeeld 3

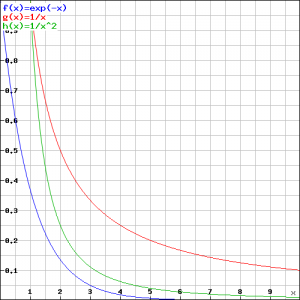
Meestal is op het oog niet snel te bepalen wanneer een oneigenlijke integraal wel of niet convergeert. Kijk bijvoorbeeld op het interval $[1,\infty]$ naar de grafieken van de volgende functies:

$f(x)=e^{-x}$

$g(x)=\displaystyle\frac{1}{x}$

$h(x)=\displaystyle\frac{1}{x^2}$

De vraag luidt nu: welke van de drie oneigenlijke integralen convergeert/divergeert?
Uit de grafiek is duidelijk dat als $g(x)$ (rood) convergeert, de andere twee dat zeker ook zullen doen. Ook zien we onmiddellijk dat $g(x)$ zal divergeren als $h(x)$ (groen) dat al doet.
Berekeningen geven de volgende resultaten.