Tweedegraads functies komen in de wiskunde vaak voor. Het is daarom goed te weten:
- dat de grafiek van een tweedegraads functie een parabool is;
- wanneer er sprake is van een dal- of bergparabool;
- hoe je het snijpunt van de parabool met de
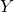 -as kunt vinden; en
-as kunt vinden; en - hoe je kunt zien of een parabool geen, een of twee punten met de
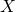 -as gemeen heeft. De discriminant speelt in dit laatste een belangrijke rol.
-as gemeen heeft. De discriminant speelt in dit laatste een belangrijke rol.
1. Gegeven de functie:
![]()
Beantwoord de volgende vragen:
- Wat is het snijpunt van de grafiek met de
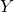 -as?
-as? - Heeft deze grafiek snijpunten met de
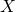 -as, en zo ja, hoeveel?
-as, en zo ja, hoeveel? - Bepaal de symmetrieas.
2. Gegeven de functie:
![]()
Beantwoord de volgende vragen:
- Voor welke waarde van
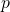 heeft deze parabool geen snijpunten met de
heeft deze parabool geen snijpunten met de 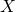 -as?
-as? - Wat is in dat geval het snijpunt met de
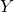 -as?
-as? - Is er dan sprake van een minimum of een maximum?
3. Gegeven de functie:
![]()
Beantwoord de volgende vragen:
- Wat is het snijpunt van de grafiek met de
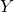 -as?
-as? - Heeft deze grafiek snijpunten met de
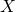 -as, en zo ja, hoeveel en bepaal de coördinaten?
-as, en zo ja, hoeveel en bepaal de coördinaten? - Wat is de symmetrie-as?
4. De vergelijking van een parabool is:
![]()
Voor welke waarde van ![]() ligt de top van deze parabool op de lijn:
ligt de top van deze parabool op de lijn:
![]()
5. De ![]() -coördinaat van de top van de parabool:
-coördinaat van de top van de parabool:
![]()
is gelijk aan ![]() .
.
Bepaal ![]() .
.
6. Voor welke waarde van ![]() heeft de parabool:
heeft de parabool:
![]()
geen snijpunten met de ![]() -as?
-as?
7. Voor welke waarde van ![]() heeft de parabool:
heeft de parabool:
![]()
twee snijpunten met de ![]() -as die op een afstand
-as die op een afstand ![]() van elkaar afliggen?
van elkaar afliggen?
8. Voor welke waarde van ![]() ligt de top van de parabool:
ligt de top van de parabool:
![]()
op de lijn:
![]()
9. Bepaal de vergelijking van de parabool die gaat door de punten ![]() ,
, ![]() en
en ![]() .
.
10. Voor welke waarde van ![]() hebben de parabolen:
hebben de parabolen:
![]()
![]()
slechts een punt gemeen.

