Quadratic functions are frequently used in mathematics. Therefore it is important to know:
- that the graph of a quadratic function is a parabola;
- when the parabola opens up or down;
- how you can quickly determine the intersection point with the
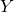 -axis; and
-axis; and - how you can find out whether the parabola has no, one or two intersection points with the
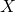 -axis and that the discriminant plays an important role.
-axis and that the discriminant plays an important role.
1. Given the function:
![]()
Answer the following questions:
- What is the intersection point of the graph and the
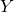 -axis?
-axis? - Do the graph and the
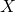 -axis have intersection points, and if so, how many?
-axis have intersection points, and if so, how many? - What is the symmetry axis?
2. Given the function:
![]()
Answer the following questions:
- For which value of
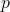 does the parabola have no intersection points with the
does the parabola have no intersection points with the 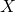 -axis?
-axis? - Calculate the intersection point with the
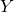 -axis.
-axis. - Does the graph has a maximum or a minimum?
3. Given the function:
![]()
Answer the following questions:
- What is the intersection point of the graph with the
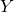 -axis?
-axis? - Does the graph have intersection points with the
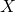 -axis, and if so, how many? Calculate the coordinates.
-axis, and if so, how many? Calculate the coordinates. - What is the symmetry axis?
4. The equation of a parabola is:
![]()
For which value of ![]() does the top of this parabola lie on the line:
does the top of this parabola lie on the line:
![]()
5. The ![]() -coordinate of the top of the parabola:
-coordinate of the top of the parabola:
![]()
is equal to ![]() .
.
Calculate ![]() .
.
6. For which value of ![]() does the parabola:
does the parabola:
![]()
have no intersection points with the ![]() -axis?
-axis?
7. For which value of ![]() does the parabola:
does the parabola:
![]()
have two intersection points with the ![]() -axis having a mutual distance of
-axis having a mutual distance of ![]() ?
?
8. For which value of ![]() does the top of the parabola:
does the top of the parabola:
![]()
lie on the line:
![]()
9. Calculate the equation of the parabola going through the points ![]() ,
, ![]() and
and ![]() .
.
10. For which value of ![]() do the parabolas:
do the parabolas:
![]()
![]()
have just one point in common.

