Samenvatting en voorbeelden
Exponentiële vergelijkingen zijn vergelijkingen waarin de onbekende variabele in de exponent voorkomt. Een eenvoudige exponentiële vergelijking ziet er bijvoorbeeld als volgt uit:
Voor het grondtal 
geldt 
en dus geldt voor de constante 
ook 
. Er zijn diverse methoden om zo'n vergelijking op te lossen.
- Wanneer het grondtal van de exponentiële vergelijking het getal a is, dan moet men de vergelijking zodanig manipuleren dat de vergelijking:
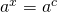
ontstaat. In dit geval is de oplossing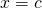
. - Wanneer methode 1 niet mogelijk is, kan de logaritme uitkomst bieden (zie ook het onderwerp Logaritmische functies en grafieken):
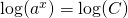
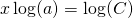
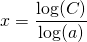
Om de berekeningen goed te kunnen uitvoeren is het heel noodzakelijk dat je goed overweg kunt met berekeningen waarin exponenten een rol spelen. Kijk hiertoe ook naar het onderwerp Rekenregels voor exponenten.
Voorbeeld 1
Los op:
We kunnen het rechter lid schrijven als:
waarmee de vergelijking wordt:
en dus geldt:
Voorbeeld 2
Los op:
We kunnen het rechter lid schrijven als:
waarmee de vergelijking wordt:
en dus geldt:
Voorbeeld 3
Los op:
We kunnen het rechter lid schrijven als:
waarmee de vergelijking wordt:
en dus geldt:
Voorbeeld 4
Los op:
Omdat we niet graag met breuken werken, schrijven we voor het linker lid:
Bovendien schrijven we voor het rechter lid:
waarmee de vergelijking wordt:
en dus geldt:
Voorbeeld 5
Los op:
We schrijven (links en rechts delen door 3):
dus:
Voorbeeld 6
Los op:
We schrijven:
Omdat we het rechter lid niet kunnen schrijven als een (rationale) macht van 3, nemen we van beide leden de logaritme:
Voorbeeld 7
Los op:
We kunnen voor het rechter lid schrijven:
en dus:
Dus we krijgen:
Voorbeeld 8
Los op:
We kunnen de vergelijking herschrijven:
Er moet dus gelden:
