Exponential equations

Summary and examples

Roughly speaking, exponential equations are equations with the unknown independent variable in some exponent. Or an equation containing one or more exponential functions, see Exponential functions and graphs. A simple exponential equation has the following general form:

The base has to satisfy the condition  and thus the same condition holds for the constant : . There are various ways to solve this kind of equation.

1. When the exponential equation has a base , we have to manipulate the equation in such a way that the following equation results:
   
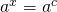
   In this case the solution is .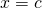
2. When this method is not possible, applying logarithms may help, see Logarithmic functions and graphs:
   
   
   

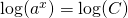
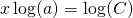
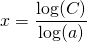
In order to carry out these calculations you need to know the Rules for exponents.

Example 1

Solve:

We can write the right-hand side as:

and thus we get the equation:

so:

Example 2

Solve:

We can write the right-hand side as:

and thus:

so:

Voorbeeld 3

Solve:

We can write the right-hand side as:

and thus:

so:

Example 4

Solve:

We do not like to work with fractions, so we rewrite the left-hand side:

Furthermore, we write for the right-hand side:

Then the equation becomes:

and thus:

Example 5

Solve:

We write after dividing both sides by :

so:

Example 6

Solve:

We write:

Because we cannot write the right-hand side as a power of , we apply the logarithmic function to both sides, see also Logarithmic functions and graphs:

Example 7

Solve:

We can write the right-hand side as:

and thus:

We get:

Example 8

Solve:

We can rewrite this equation:

and thus: