Eerstegraads functies en grafieken

Samenvatting en voorbeelden

De algemene vergelijking van een eerstegraads functie is:

$y=ax+b$

De $a$ en $b$ zijn willekeurige constanten en worden ook wel parameters genoemd.

Omdat de grafiek van deze functie een rechte lijn is, wordt een dergelijke functie ook wel een lineaire functie genoemd.

De parameters $a$ en $b$ hebben een duidelijke betekenis. De $a$ is de richtingscoëfficiënt of hellingsgetal (in het Engels: slope) van de lijn en is een maat voor de helling van de lijn. Er geldt:

$a>0$ : de lijn loopt van linksonder naar rechtsboven;
$a<0$ : de lijn loopt van linksboven naar rechtsonder;
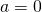$a=0$ : de lijn loopt evenwijdig aan de horizontale as, meestal de X-as genoemd.

De parameter $b$ bepaalt de $y$ -coördinaat van het snijpunt van de lijn met de verticale as, meestal de $Y$ -as genoemd.

Overigens, het is belangrijk te weten dat de richtingscoëfficiënt $a$ het quotiënt is van de toename van $y$ ten gevolge van een toename van $x$ . Dus:

$a=\displaystyle\frac{\Delta y}{\Delta x}$

De teller geeft de toename van $y$ weer, de noemer die van $x$ .

Voorbeeld 1

Teken de lijn:

$l: y=2x+5$

en bepaal de richtingscoëfficiënt en het exacte snijpunt van de lijn met de $Y$ -as.
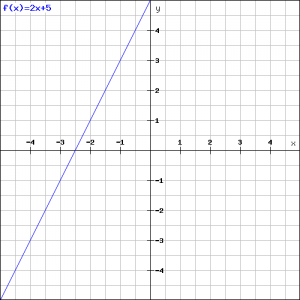
In de figuur is de grafiek van deze functie getekend.

Het snijpunt van de lijn met de $Y$ -as is (0,5), en de richtingscoëfficiënt van de lijn is 2. We zouden de lijn nu kunnen tekenen, maar om de lijn te kunnen tekenen is een richtingscoëfficiënt niet zo handig. Het is beter een tweede punt te vinden. Immers, wanneer je twee punten hebt, kun je de lijn zo tekenen. We proberen het snijpunt van de lijn met de $X$ -as te berekenen. Voor elk punt op de $X$ -as geldt: $y=0$ . Dus de lijn snijdt de $X$ -as wanneer geldt:

$0=2x+5$
$x=-2.5$

Het snijpunt van de lijn met de $X$ -as is dus: (-2.5,0).

Nu we de twee punten (0,5) en (-2.5,0) hebben is de grafiek van de lijn onmiddellijk te tekenen.

Voorbeeld 2

Teken de lijn:

$l: y=-x+2$

en bepaal de richtingscoëfficiënt en het exacte snijpunt van de lijn met de $Y$ -as.

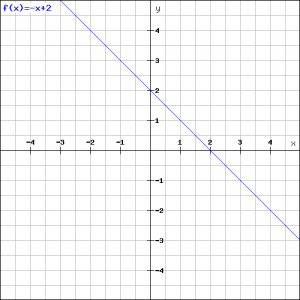
In de figuur is de grafiek van de functie getekend.

De gemakkelijkste manier om de lijn te kunnen tekenen is twee punten te vinden die op die lijn liggen. Het eerste punt is (0,2) omdat $b=2$ . Het tweede punt is gemakkelijk te berekenen door y=0 te kiezen:

$0=-x+2$
$x=2$

en dus is het tweede punt (2,0).

De lijn kan nu gemakkelijk worden getekend.

Voorbeeld 3

Lijnen kunnen elkaar snijden. Ze hebben dan een snijpunt.

Bereken de coördinaten van het snijpunt van de lijnen uit voorbeeld 1 en 2:

$l: y=2x+5$
$m: y=-x+2$

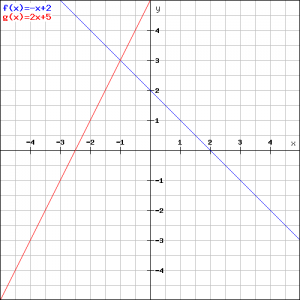
In de figuur zijn beide lijnen nogmaals getekend.

Voor het snijpunt S geldt dat de $y$ -coördinaten van de samenvallende punten gelijk zijn. Wanneer de $y$ - coördinaten gelijk zijn, moeten de rechter leden ook gelijk zijn en dat levert de volgende vergelijking op:

$2x+5=-x+2$
$3x=-3$
$x=-1$

De $x$ -coördinaat van het punt S is dus -1 en dus is de $y$ -coördinaat gelijk aan $y=3$ (de waarde $x=-1$ invullen in een van de vergelijkingen). De coördinaten van S zijn dus (-1,3), wat ook is af te lezen uit de figuur.

Voorbeeld 4

Geef de formule van de lijn die door het punt P(1,3) gaat en richtingscoëfficiënt 2 heeft.
Deze opgave kan op de volgende manier worden aangepakt. De algemene formule voor een lijn is:

$y=ax+b$

Omdat de richtingscoëfficiënt $2$ is geldt:

$a=2$

Het punt P(1,3) ligt op de lijn en dus moet gelden:

$3=2.1+b$
$b=1$

en dus is de vergelijking van de gevraagde lijn:

$y=2x+1$

Een andere aanpak is het onthouden van een eenvoudige formule die ontstaat door het voorgaande toe te passen voor een willekeurig punt:

$P(x_p,y_p)$ . In dit geval geldt: $x_p=1$ en $y_p=3$ .

en een richtingscoëfficiënt $m$ . In dit geval geldt $m=2$ .

De formule van de gevraagde lijn is dan:

$y-y_p=m(x-x_p)$

Passen we deze formule toe bij de eerdere opgave, dan krijgen we:

$y-3=2(x-1)$
$y=2x+1$

Voorbeeld 5

Bereken de formule van de lijn die gaat door P(1,2) en Q(-1,1).

De richtingscoëfficiënt van de lijn zal moeten zijn:

$m=\displaystyle\frac{y_Q-y_P}{x_Q-x_P}$

Immers, $m$ is de toename van $y$ gedeeld door de toename van $x$ ; hierboven gerekend uitgaande van het punt P.

Omdat de lijn door zowel P als Q gaat kunnen we de formule uit voorbeeld 4 toepassen door met de gevonden richtingscoëfficiënt een van deze punten te gebruiken. We kiezen nu voor P en dus krijgen we:

$y-2=\displaystyle\frac{1}{2}(x-1)$
$y=\displaystyle\frac{1}{2}x+\displaystyle\frac{3}{2}$

Het resultaat zou hetzelfde zijn geweest wanneer we de formule zouden hebben toegepast met punt Q.

Voorbeeld 6

We hebben twee lijnen:

$l: y=2x-1$
$m: y=ax+b$

Voor welke waarden van $a$ en $b$ hebben deze twee lijnen:

geen snijpunt;
één snijpunt.

De lijnen hebben geen snijpunt (dat wil zeggen geen gemeenschappelijk punt) wanneer ze evenwijdig lopen. In dat geval moet gelden:

$a=2$ en $b\neq-1$

Immers als $a=2$ dan hebben beide lijnen dezelfde richtingscoëfficiënt en lopen ze evenwijdig of vallen ze samen. Ze vallen samen wanneer ook nog geldt $b=-1$ ; in dat geval hebben ze oneindig veel punten gemeen.

De lijnen hebben slechts één snijpunt gemeen als:

$a\neq2$

en $b$ mag dan elke waarde aannemen.

Voorbeeld 7

In voorbeeld 3 hebben we gezien hoe we een snijpunt van twee lijnen:

$l: y=2x+5$
$m: y=-x+2$

hebben berekend.

We herschrijven de formules van beide lijnen op de volgende wijze:

$2x-y=-5$
$x+y=2$

Het vinden van de oplossing voor $x$ en $y$ van deze vergelijkingen staat bekend als het oplossen van twee lineaire vergelijkingen met twee onbekenden. De aanpak is doorgaans dat een van de variabelen wordt geëlimineerd. In dit geval kiezen we voor eliminatie van $y$ omdat door het optellen van beide vergelijkingen de y inderdaad verdwijnt:

$3x=-3$
$x=-1$

Substitutie van deze waarde van $x$ in een van de vergelijkingen levert de waarde van $y=3$ op.