Summary and examples
The general formula of a linear function is:
![]()
![]() and
and ![]() are arbitrary constants and are also called parameters.
are arbitrary constants and are also called parameters.
The function is called linear because its graph is a straight line.
The parameters ![]() and
and ![]() have a meaning. The
have a meaning. The ![]() is the slope of the line.
is the slope of the line.
We distinguish:
 : the line goes from lower left to upper right;
: the line goes from lower left to upper right; : the line goes from upper left to lower right;
: the line goes from upper left to lower right;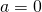 : the line is horizontal, so parallel to the X-axis.
: the line is horizontal, so parallel to the X-axis.
The parameter ![]() is the
is the ![]() -coordinate of the intersection point of the line with the vertical axis, usually called the
-coordinate of the intersection point of the line with the vertical axis, usually called the ![]() -axis.
-axis.
Note that the slope ![]() is the quotient of the
is the quotient of the ![]() -increment and the increment of
-increment and the increment of ![]() . So:
. So:
![]()
The numerator represents the increment of ![]() , the denominator the increment of
, the denominator the increment of ![]() .
.
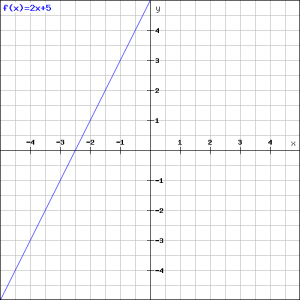
Example 1
Draw the line:
![]()
and determine the slope and the exact intersection point of the line and the ![]() -axis.
-axis.
In the figure the graph of this function is outlined.
The intersection point of the line with the ![]() -axis is
-axis is ![]() , and its slope is
, and its slope is ![]() . This is enough information to draw the line, but a slope is difficult to use. It would be easier to draw the line if we would have two points on the line. We try to calculate the intersection point of the line with the
. This is enough information to draw the line, but a slope is difficult to use. It would be easier to draw the line if we would have two points on the line. We try to calculate the intersection point of the line with the ![]() -axis. For each point on the
-axis. For each point on the ![]() -axis we have
-axis we have ![]() . So the line intersects the
. So the line intersects the ![]() -axis if:
-axis if:
![]()
![]()
Thus the intersection point of the line with the ![]() -axis is:
-axis is: ![]() .
.
Now we have two points ![]() and
and ![]() on the line we can draw the line.
on the line we can draw the line.
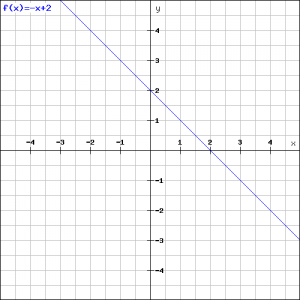
Example 2
Draw the line:
![]()
and determine its slope and the exact intersection point with the ![]() -axis.
-axis.
In the figure the graph of the function is drawn.
The easiest way to draw the line is to find two points on it. The first point is ![]() because
because ![]() . We find the second point by taking
. We find the second point by taking ![]() :
:
![]()
![]()
and so the second point is ![]() .
.
Now the line can be easily drawn.
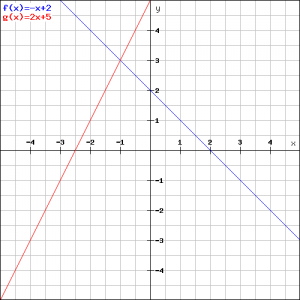
Example 3
Lines can intersect. Then they have an intersection point.
Calculate the coordinates of the intersection point of the lines of example 1 and 2:
![]()
![]()
In the figure both lines are drawn again.
In the intersection point ![]() the two
the two ![]() -coordinates are equal. Then the right-hand sides have to be equal as well resulting in the following equation:
-coordinates are equal. Then the right-hand sides have to be equal as well resulting in the following equation:
![]()
![]()
![]()
Then the ![]() -coordinate of
-coordinate of ![]() is
is ![]() and thus the
and thus the ![]() -coordinate is equal to
-coordinate is equal to ![]() (substitute the value
(substitute the value ![]() in one of the equations). So the coordinates of
in one of the equations). So the coordinates of ![]() are
are ![]() see the figure.
see the figure.
Example 4
Give the formula of the line though the point ![]() with slope
with slope ![]() .
.
This assignment can be solved in two ways.
The general formula of the line is:
![]()
Since the slope equals ![]() we have:
we have:
![]()
The point ![]() is on the line so:
is on the line so:
![]()
![]()
and thus the equation of the line is:
![]()
Another way to solve this assignment is to apply a simple formula for any point ![]() .
.
In this case we have: ![]() and
and ![]() and the slope is
and the slope is ![]() .
.
The formula of the line is:
![]()
When we apply this formula, we get:
![]()
![]()
Example 5
Calculate the formula of the line which goes through the points ![]() and
and ![]() .
.
The slope of the line equals:
![]()
![]() is the increment of
is the increment of ![]() divided by the increment of
divided by the increment of ![]() ; in this example the points
; in this example the points ![]() and
and ![]() are used.
are used.
Because the line goes through both ![]() and
and ![]() we can apply the formula from example 4. We choose the point
we can apply the formula from example 4. We choose the point ![]() and get:
and get:
![]()
![]()
The result would have been the same if the point ![]() was taken.
was taken.
Example 6
We have the following two lines:
![]()
![]()
For which values of ![]() and
and ![]() do these lines have:
do these lines have:
- no intersection point;
- one intersection point.
The lines have no intersection point when they are parallel. Then we have:
![]() and
and ![]()
If ![]() these lines have the same slope and then they are parallel or coincide. They coincide if in addition
these lines have the same slope and then they are parallel or coincide. They coincide if in addition ![]() ; then they have an infinite number of points in common.
; then they have an infinite number of points in common.
The lines have just one intersection point if:
![]()
and then ![]() may take any value.
may take any value.
Example 7
In example 3 we saw how we could calculate the intersection point of two lines:
![]()
![]()
We rewrite the formulas of both lines in the following way:
![]()
![]()
Solving the values of ![]() and
and ![]() of this is known as solving two linear equations with two variables.
of this is known as solving two linear equations with two variables.
Usually we solve this by eliminating one of the two variables. In this case we choose to eliminate ![]() because the variable
because the variable ![]() is eliminated by adding both equations:
is eliminated by adding both equations:
![]()
![]()
When we substitute this value of ![]() in one of the equations we get the value of
in one of the equations we get the value of ![]() .
.