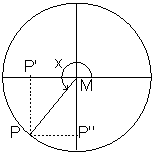Summary and examples
We will define the following three standard functions from trigonometry: ![]() ,
, ![]() and
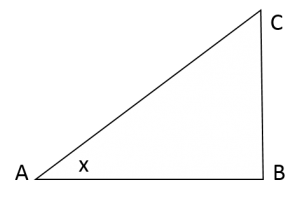
and ![]() . We do this by using a right-angled triangle
. We do this by using a right-angled triangle ![]() . We call the angle
. We call the angle ![]()
![]() , see the figure:
, see the figure:
Remember that ![]() .
. ![]() is the angle either in degrees or radians (see later for this).
is the angle either in degrees or radians (see later for this).
In the figure the angle is an acute angle ![]() , so
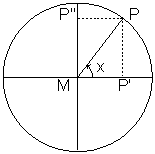
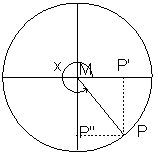
, so ![]() . When the angle is outside this interval these definitions cannot be used. That is why we use the unit circle, i.e. a circle with center
. When the angle is outside this interval these definitions cannot be used. That is why we use the unit circle, i.e. a circle with center ![]() and radius
and radius ![]() . Now we see that
. Now we see that ![]() is equal to the angle
is equal to the angle ![]() .
.
Now ![]() can be defined as the projection of
can be defined as the projection of ![]() on the
on the ![]() -axis and
-axis and ![]() as the projection of
as the projection of ![]() on the
on the ![]() -axis. These definitions allow us to define
-axis. These definitions allow us to define ![]() and
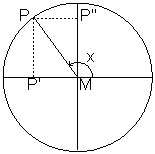
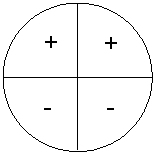
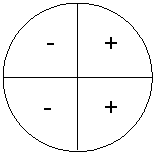
and ![]() functions also for other angles than acute angles. In the figures below various angles are shown with
functions also for other angles than acute angles. In the figures below various angles are shown with ![]() in the second, third and fourth quadrant, respectively.
in the second, third and fourth quadrant, respectively.
We see that ![]() is positive, negative, negative, respectively. For
is positive, negative, negative, respectively. For ![]() we have negative, negative, positive, respectively.
we have negative, negative, positive, respectively.
We can show this in the following figures:
 | ||
 |
From these figures we can deduce some simple and well-known formulas.
![]()
![]()
Later we will show a few other simple formulas based on the unit circle, but first we will introduce the radian which is another unit for angles. The relationship between an angle in degrees and an angle in radians is:
360 degrees= ![]() radians (in brief rads)
radians (in brief rads)
and thus we have:
1 rad = ![]() degrees
degrees
Following we will use radians unless mentioned otherwise. We will give some more formulas that can easily be deduced from the unit circle (sometimes we use congruent triangles).
![]()
![]()
To calculate the ![]() of an arbitrary angle
of an arbitrary angle ![]() , we usually need a calculator (remember to put it in the radians mode when the angles are given in radians). For a few special angles, we use the following table:
, we usually need a calculator (remember to put it in the radians mode when the angles are given in radians). For a few special angles, we use the following table:
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
You can recall this table easily by remembering the first row (the ![]() -row), where the number under the root sign is subsequently
-row), where the number under the root sign is subsequently ![]() and
and ![]() . The
. The ![]() -row can be used in a similar way, though from right to left. We get the
-row can be used in a similar way, though from right to left. We get the ![]() -row by dividing the
-row by dividing the ![]() -row by the
-row by the ![]() -row.
-row.
Now we have defined the ![]() - and
- and ![]() -function, we can summarize a number of properties.
-function, we can summarize a number of properties.
The period of this function is equal to The function has zeros (is equal to | |
The period of this function is equal to The function has zeros for |
Earlier we mentioned a number of simple formulas. A few formulas occur so frequently that you can better learn them by heart:
![]()
![]()
![]()
![]()
The latter formula can be written in another form by using the first formula:
![]()
![]()
The first two formulas can easily be deduced from earlier given definitions. We know that:
![]()
![]()
and thus:
![]()
![]()
We used the Pythagoras' Theorem.
The second formula can also be deduced easily:
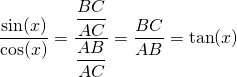
Finally, there are a number of formulas that are less frequently used. Then it does not really pay to remember them heart. Sometimes they are necessary, but then a formula sheet can be used.
Example 1
Explain using the unit circle that the following formula holds (angle ![]() in degrees):
in degrees):
![]()
The angle ![]() degrees can be written as
degrees can be written as ![]() degrees.
degrees.
The projection of ![]() with
with ![]() degrees on the
degrees on the ![]() -axis is equal to the projection of
-axis is equal to the projection of ![]() with
with ![]() degrees on de
degrees on de ![]() -axis. This can be proven by congruence of triangles. So this relation is valid.
-axis. This can be proven by congruence of triangles. So this relation is valid.
Example 2
Explain using the unit circle that the following formula holds (angle ![]() in radians):
in radians):
![]()
This formula is the same as in example 1, though formulated more generally. Again, this can be proven using the congruence of triangles.
Example 3
Calculate without a calculator ![]() , the angle is given in degrees.
, the angle is given in degrees.
We can write the formula as ![]() and thus the angle is in the third quadrant. We notice that
and thus the angle is in the third quadrant. We notice that ![]() and this value can be found in the table:
and this value can be found in the table:
![]()
Example 4
Prove:
![]()
The left-hand side can be written as:
![]()
We know that:
![]()
![]()
and thus the relation is proven.