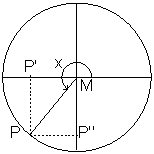Samenvatting en voorbeelden
We zullen drie basisfuncties (![]() ,
, ![]() en
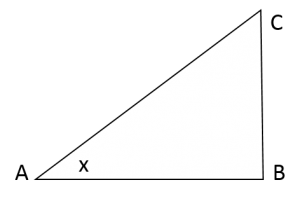
en ![]() ) uit de goniometrie definiëren en doen dat met behulp van een rechthoekige driehoek
) uit de goniometrie definiëren en doen dat met behulp van een rechthoekige driehoek ![]() . We bekijken de hoek
. We bekijken de hoek ![]() en noemen die
en noemen die ![]() , zie de figuur:
, zie de figuur:
|
 |
![]() is de hoek in graden of radialen (zie later voor dit begrip).
is de hoek in graden of radialen (zie later voor dit begrip).
In de figuur is de hoek ![]() een scherpe hoek, dus
een scherpe hoek, dus ![]() . Wanneer de hoek buiten deze grenzen valt, is de definitie moeilijker te hanteren. Daarom gebruiken we de eenheidscirkel, dat wil zeggen een cirkel met straal gelijk aan
. Wanneer de hoek buiten deze grenzen valt, is de definitie moeilijker te hanteren. Daarom gebruiken we de eenheidscirkel, dat wil zeggen een cirkel met straal gelijk aan ![]() . We zien dat
. We zien dat ![]() gelijk is aan hoek
gelijk is aan hoek ![]() .
.
|
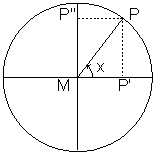 |
![]() kan dus worden gedefinieerd als de projectie van
kan dus worden gedefinieerd als de projectie van ![]() op de
op de ![]() -as en
-as en ![]() als de projectie van
als de projectie van ![]() op de
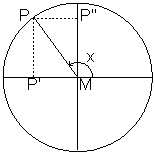
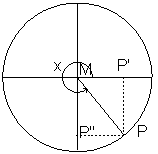
op de ![]() -as. Op deze manier kunnen we nu ook gemakkelijk andere hoeken dan scherpe hoeken definiëren. In de onderstaande figuur worden diverse hoeken getoond met
-as. Op deze manier kunnen we nu ook gemakkelijk andere hoeken dan scherpe hoeken definiëren. In de onderstaande figuur worden diverse hoeken getoond met ![]() in respectievelijk het tweede, derde en vierde kwadrant.
in respectievelijk het tweede, derde en vierde kwadrant.
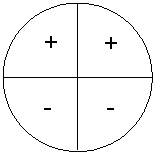
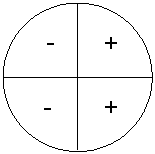
We zien dat ![]() achtereenvolgens positief, negatief, negatief is. Voor
achtereenvolgens positief, negatief, negatief is. Voor ![]() geldt achtereenvolgens negatief, negatief, positief. We kunnen dat laten zien in de volgende figuren:
geldt achtereenvolgens negatief, negatief, positief. We kunnen dat laten zien in de volgende figuren:
Een paar eenvoudige formules kunnen uit de voorgaande figuren worden afgeleid.
![]()
![]()
Later zullen we nog een paar andere eenvoudige formules kunnen laten zien aan de hand van de eenheidscirkel, maar eerst zullen we de radiaal introduceren. De radiaal is een andere eenheid voor een hoek. De relatie tussen een hoek in graden en een hoek in radialen is:
360 graden = ![]() radialen
radialen
en dus geldt:
1 rad = ![]() graden
graden
In het vervolg zullen we met radialen werken, tenzij anders aangegeven.
We zullen nog een paar formules geven die eenvoudig kunnen worden afgeleid uit de bovenstaande eenheidscirkels (denk hierbij aan de congruentie van driehoeken).
![]()
![]()
Om van een willekeurige hoek ![]() de sin uit te rekenen, hebben we een rekenmachine nodig (denk erom hem op radialen te zetten wanneer de hoeken in radialen worden gegeven). Voor een paar bijzondere hoeken gebruiken we de volgende tabel:
de sin uit te rekenen, hebben we een rekenmachine nodig (denk erom hem op radialen te zetten wanneer de hoeken in radialen worden gegeven). Voor een paar bijzondere hoeken gebruiken we de volgende tabel:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
Deze tabel is het gemakkelijkst te onthouden door de eerste rij (de ![]() -rij) te onthouden, waar het getal onder het wortelteken achtereenvolgens
-rij) te onthouden, waar het getal onder het wortelteken achtereenvolgens ![]() en
en ![]() is. De
is. De ![]() -rij werkt identiek, maar dan van rechts naar links. De
-rij werkt identiek, maar dan van rechts naar links. De ![]() -rij krijg je door de
-rij krijg je door de ![]() -rij te delen door de
-rij te delen door de ![]() -rij.
-rij.
Nu we de ![]() - en
- en ![]() -functie hebben gedefinieerd, kunnen we een paar eigenschappen noemen.
-functie hebben gedefinieerd, kunnen we een paar eigenschappen noemen.
De periode van deze functie is gelijk aan De functie heeft nulpunten voor |
|
De periode van deze functie is gelijk aan De functie heeft nulpunten voor |
We hebben al een paar eenvoudige formules gezien. Een paar formules komen zo vaak voor dat ze het beste uit het hoofd kunnen worden geleerd:
![]()
![]()
![]()
![]()
De laatste formule kan met behulp van de eerste formule worden geschreven als:
![]()
![]()
De eerste twee formules kunnen gemakkelijk worden afgeleid uit de eerder gegeven definities. We weten dat:
![]()
![]()
en dus:
![]()
In deze berekening is gebruik gemaakt van de stelling van Pythagoras.
Ook de tweede formule kan gemakkelijk worden afgeleid:
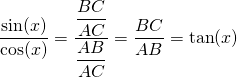
Tenslotte is er nog een aantal formules die doorgaans minder vaak worden gebruikt. Dan loont het niet echt ze uit het hoofd te leren. Bij sommige opgaven zijn ze wel nodig, maar dan kan een formuleblad worden gebruikt.
Voorbeeld 1
Beredeneer met behulp van de eenheidscirkel dat de volgende formule geldt (hoek ![]() in graden):
in graden):
![]()
De hoek ![]() graden kan worden geschreven als
graden kan worden geschreven als ![]() graden.
graden.
De projectie van ![]() bij
bij ![]() graden op de
graden op de ![]() -as is gelijk aan de projectie van
-as is gelijk aan de projectie van ![]() bij
bij ![]() graden op de
graden op de ![]() -as. Dit kan met behulp van congruentie van rechthoekige driehoeken worden aangetoond. Dus is de gevraagde relatie geldig.
-as. Dit kan met behulp van congruentie van rechthoekige driehoeken worden aangetoond. Dus is de gevraagde relatie geldig.
Voorbeeld 2
Beredeneer met behulp van de eenheidscirkel dat de volgende formule geldt (hoek ![]() in radialen):
in radialen):
![]()
Deze formule is in feite dezelfde als in voorbeeld ![]() , nu echter in het algemeen geformuleerd. Ook nu kan met behulp van congruentie van driehoeken de relatie worden bewezen.
, nu echter in het algemeen geformuleerd. Ook nu kan met behulp van congruentie van driehoeken de relatie worden bewezen.
Voorbeeld 3
Bereken zonder rekenmachine ![]() , de hoek is gegeven in graden.
, de hoek is gegeven in graden.
Deze hoek kunnen we schrijven als ![]() en is dus een hoek in het derde kwadrant. We zien dus dat
en is dus een hoek in het derde kwadrant. We zien dus dat ![]() en deze kunnen we vinden in de tabel:
en deze kunnen we vinden in de tabel:
![]()
Voorbeeld 4
Bewijs dat geldt:
![]()
We werken het linkerlid uit en krijgen:
![]()
We weten dat:
![]()
![]()
waarmee het gevraagde is aangetoond.