Optimizing f(x,y)

Summary and examples

The graph of a function $y=f(x)$ may have one or more local extremes: maxima or minima. These can be found by taking the derivative $f'(x)$ and solving the equation $f(x)=0$ . This yields values of $x$ for which the function may have a maximum or minimum. However, it is not sure that such a value of $x$ yields a maximum or minimum. It is also possible that the graph for such a value of $x$ has a horizontal inflection point. Further research is necessary. More information about this can be found in Optimizing $f(x)$ .

A similar approach is chosen for finding local extremes of graphs of functions with two independent variables $z=f(x,y)$ . In order to find points $(x,y)$ for which $f(x,y)$ has an extremum we determine the partial derivatives $\displaystyle\frac{\partial{f}}{\partial{x}}$ and $\displaystyle\frac{\partial{f}}{\partial{y}}$ and solve the equations $\displaystyle\frac{\partial{f}}{\partial{x}}=0$ and $\displaystyle\frac{\partial{f}}{\partial{y}}=0$ . The solutions of these two equations are called stationary solutions. Also in this case it is not sure that a stationary point $(x,y)$ yields a maximum or a minimum. Such a point may also yield a saddle point.
Similar to optimizing $y=f(x)$ there are methods to find out whether a stationary point of $f(x,y)$ is a maximum, a minimum or a saddle point.

In the following we use the notation for a partial derivative: $\frac{\partial{f}}{\partial{x}}=f_x$ .

In order to find out the nature of a stationary point we follow this procedure:

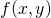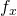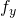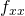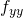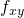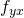Calculate all first order, second order and mixed second order partial derivatives of $f(x,y)$ : $f_x$ , $f_y$ , $f_{xx}$ , $f_{yy}$ , $f_{xy}$ and $f_{yx}$ . All of them are needed in the following steps.
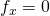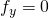Solve the equations: $f_x=0$ and $f_y=0$ and suppose that 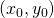$(x_0,y_0)$ is a solution, thus a stationary point.
Calculate: 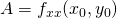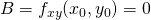$A=f_{xx}(x_0,y_0)$ , $B=f_{xy}(x_0,y_0)=0$ and $C=f_{yy}(x_0,y_0)$ .
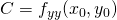Calculate: $\Delta=AC-B^2$ .

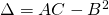Now we may conclude (see also Essential Mathematics for Economic Analysis by: Sydsaeter and Hammond, 4th ed):
a. If $\Delta>0$ and $A<0$ , then $(x_0,y_0)$ is a local maximum;
b. If $\Delta>0$ and $A>0$ , then $(x_0,y_0)$ is a local minimum;
c. If $\Delta<0$ , then $(x_0,y_0)$ is a saddle point;
d. If $\Delta=0$ , then $(x_0,y_0)$ may be a local maximum, a local minimum or a saddle point.

Example 1

Calculate the stationary points of:

$f(x,y)=x^3-x^2-y^2+8$

and determine its nature.

We follow the procedure.

$f_x=3x^2-2x$

$f_y=-2y$

$f_{xx}=6x-2$

$f_{yy}=-2$

$f_{xy}=0$

We solve the equation: $f_x=0$ and $f_y=0$ :

$f_x=3x^2-2x=0$ , so $x=0$ or $x=\displaystyle\frac{2}{3}$

$f_y=-2y=0$ , so $y=0$

The stationary points are thus: $(0,0)$ and $(\displaystyle\frac{2}{3},0)$

3. and 4.

For $\displaystyle(0,0)$ we have: $A=-2$ , $B=0$ , $C=-2$ thus $\Delta=4$ .

For $\displaystyle(\frac{2}{3},0)$ we have: $A=2$ , $B=0$ , $C=-2$ thus $\Delta=-4$ .

We may conclude that $(0,0)$ is a local maximum and $(\displaystyle\frac{2}{3},0)$ is a saddle point.

Example 2

A perfectly competitive firm produces two goods, $X$ and $Y$ which are sold at $54$ and $52$ euro per unit, respectively. The firm has a total cost function given by ( $x$ is the number of units of good $X$ and $y$ the number of units of good $Y$ ):

$TC=3x^2+3xy+2y^2-100$

Find the quantities of each good which must be produced and sold in order to maximize profits (from Bradley T. en Patton P., Essential Mathematics for Economics and Business, 4th ed).

The profit is the revenue $(R)$ minus total costs $(TC)$ .