Samenvatting en voorbeelden
De grafiek van een functie ![]() kan een of meer lokale extremen hebben: maxima of minima. Deze kunnen worden gevonden door de afgeleide
kan een of meer lokale extremen hebben: maxima of minima. Deze kunnen worden gevonden door de afgeleide ![]() te berekenen en de vergelijking
te berekenen en de vergelijking ![]() op te lossen. Dit levert waarden van
op te lossen. Dit levert waarden van ![]() waarvoor de functie een maximum of een minimum kan hebben. Het is evenwel niet zeker of een gevonden waarde van
waarvoor de functie een maximum of een minimum kan hebben. Het is evenwel niet zeker of een gevonden waarde van ![]() een maximum of een minimum oplevert en het is zelfs niet zeker dat er sprake is van een maximum of een minimum. Het is ook mogelijk dat de grafiek voor zo’n waarde van
een maximum of een minimum oplevert en het is zelfs niet zeker dat er sprake is van een maximum of een minimum. Het is ook mogelijk dat de grafiek voor zo’n waarde van ![]() een horizontaal buigpunt heeft. Nader onderzoek moet dan uitsluitsel bieden. Meer informatie hierover kan worden gevonden in Optimaliseren
een horizontaal buigpunt heeft. Nader onderzoek moet dan uitsluitsel bieden. Meer informatie hierover kan worden gevonden in Optimaliseren ![]() .
.
Een vergelijkbare aanpak wordt gekozen voor het vinden van lokale extremen van grafieken van functies met twee onafhankelijke variabelen: ![]() . Om punten
. Om punten ![]() te vinden waarvoor
te vinden waarvoor ![]() een extreem heeft worden de partiële afgeleiden
een extreem heeft worden de partiële afgeleiden ![]() en
en ![]() berekend en de vergelijkingen
berekend en de vergelijkingen ![]() en
en ![]() opgelost. De oplossingen van deze twee vergelijkingen, dat wil zeggen die punten
opgelost. De oplossingen van deze twee vergelijkingen, dat wil zeggen die punten ![]() die voldoen aan beide vergelijkingen, worden stationaire punten genoemd. Ook in dit geval is het niet zeker dat een gevonden oplossing
die voldoen aan beide vergelijkingen, worden stationaire punten genoemd. Ook in dit geval is het niet zeker dat een gevonden oplossing ![]() een maximum of een minimum oplevert en het is zelfs niet zeker dat er sprake is van een maximum of een minimum. Er zijn allerlei alternatieven mogelijk, waarvan het zadelpunt misschien wel het bekendste is. Net zoals dat het geval is bij optimaliseren van
een maximum of een minimum oplevert en het is zelfs niet zeker dat er sprake is van een maximum of een minimum. Er zijn allerlei alternatieven mogelijk, waarvan het zadelpunt misschien wel het bekendste is. Net zoals dat het geval is bij optimaliseren van ![]() zijn er ook bij het optimaliseren van
zijn er ook bij het optimaliseren van ![]() methoden om te bepalen of er sprake is van een extreem.
methoden om te bepalen of er sprake is van een extreem.
Voor partiële afgeleiden wordt ook wel een andere notatie gebruikt die we hier zullen toepassen: ![]() .
.
De volgende procedure kan worden gevolgd om duidelijkheid te krijgen over de aard van de stationaire oplossing:
- Bereken alle partiële afgeleiden van
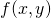 :
: 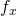 ,
, 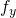 ,
, 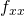 ,
, 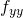 ,
, 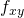 en
en 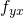 . Deze zijn in het vervolg alle nodig en het is daarom nuttig ze alvast te hebben berekend.
. Deze zijn in het vervolg alle nodig en het is daarom nuttig ze alvast te hebben berekend. - Los de vergelijkingen op:
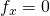 en
en 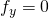 . Neem aan dat
. Neem aan dat 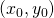 een oplossing is, dus een stationaire waarde.
een oplossing is, dus een stationaire waarde. - Bereken:
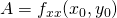 ,
, 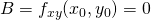 en
en 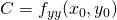 .
. - Bereken:
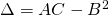 .
.
Nu kunnen we de volgende conclusies trekken:
a. Als ![]() en
en ![]() , dan is
, dan is![]() een lokaal maximum;
een lokaal maximum;
b. Als ![]() en
en ![]() , dan is
, dan is ![]() een lokaal minimum;
een lokaal minimum;
c. Als ![]() , dan is
, dan is ![]() een zadelpunt;
een zadelpunt;
d. Als ![]() , dan kan
, dan kan ![]() een lokaal maximum, een lokaal minimum of een zadelpunt zijn.
een lokaal maximum, een lokaal minimum of een zadelpunt zijn.
Het is een ingewikkeld verhaal, maar biedt een uitstekende leidraad om optimaliseringsproblemen op te lossen.
Voorbeeld 1
Bereken de stationaire punten van:
![]()
en geef aan om wat voor punten het gaat.
We lopen de punten langs.
1.
![]()
![]()
![]()
![]()
![]()
2.
We lossen de vergelijkingen ![]() en
en ![]() op:
op:
![]() , dus
, dus ![]() of
of ![]()
![]() , dus
, dus ![]()
De stationaire waarden zijn dus: ![]() en
en ![]()
3. en 4.
Voor ![]() geldt:
geldt: ![]() ,
, ![]() ,
, ![]() en dus
en dus ![]() .
.
Voor ![]() geldt:
geldt: ![]() ,
, ![]() ,
, ![]() en dus
en dus ![]() .
.
We kunnen dus concluderen dat ![]() een lokaal maximum is en
een lokaal maximum is en ![]() een zadelpunt.
een zadelpunt.
Voorbeeld 2
Een bedrijf produceert twee goederen ![]() en
en ![]() die worden verkocht voor respectievelijk
die worden verkocht voor respectievelijk ![]() en
en ![]() euro per stuk. De totale kostenfunctie van dit bedrijf is (
euro per stuk. De totale kostenfunctie van dit bedrijf is (![]() is het aantal stuks van goed
is het aantal stuks van goed ![]() en
en ![]() is het aantal stuks van goed
is het aantal stuks van goed ![]() ):
):
![]()
Welke aantallen goederen ![]() en
en ![]() moeten worden geproduceerd en verkocht om de winst te maximaliseren? (Ontleend aan Bradley T. en Patton P., Essential Mathematics for Economics and Business.)
moeten worden geproduceerd en verkocht om de winst te maximaliseren? (Ontleend aan Bradley T. en Patton P., Essential Mathematics for Economics and Business.)
De winst wordt vastgesteld door te berekenen: omzet ![]() minus de totale kosten
minus de totale kosten ![]() .
.
De omzet is:
![]()
De winst is derhalve:
![]()
Gevraagd wordt nu dus ![]() te optimaliseren en we doorlopen daartoe de eerder genoemde stappen:
te optimaliseren en we doorlopen daartoe de eerder genoemde stappen:
1.
![]()
![]()
![]()
![]()
![]()
2.
We lossen de vergelijkingen ![]() en
en ![]() op:
op:
![]()
![]()
Deze twee vergelijkingen leveren de oplossing: ![]() en
en ![]() .
.
3. en 4.
We vinden:
![]() ,
, ![]() ,
, ![]() en dus
en dus ![]()
We kunnen dus concluderen dat de maximum winst gelijk is aan ![]() voor
voor ![]() en
en ![]() .
.

