Summary and examples
The general equation of a quadratic function is:
![]()
![]() ,
, ![]() and
and ![]() are called parameters.
are called parameters. ![]() , because otherwise it is no quadratic function.
, because otherwise it is no quadratic function.
The graph of a quadratic function is a parabola. There are two types, one that opens up and one that opens down, depending on the parameter ![]() .
.
![]() : opens up
: opens up
![]() : opens down
: opens down
A parabola intersects the ![]() -axis in the point
-axis in the point ![]() . You can easily see this, because for any point on the
. You can easily see this, because for any point on the ![]() -axis we have
-axis we have ![]() . When
. When ![]() is substituted in the equation we get
is substituted in the equation we get ![]() .
.
When a parabola intersects the ![]() -axis we can calculate the intersection points in various ways. The
-axis we can calculate the intersection points in various ways. The ![]() -formula, explained in Quadratic equations (abc-formula), always gives a solution. Another way is based on factorizing the equation, see the topic Quadratic equations (factorizing). This is faster, though not always possible.
-formula, explained in Quadratic equations (abc-formula), always gives a solution. Another way is based on factorizing the equation, see the topic Quadratic equations (factorizing). This is faster, though not always possible.
The intersection points can be calculated by applying the ![]() -formula:
-formula:
![]()
In this formula the discrriminant plays an important role:
![]()
We have:
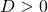 : the parabola has two different intersection points with the
: the parabola has two different intersection points with the  -axis;
-axis;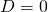 : the parabola has two coinciding intersection points with the
: the parabola has two coinciding intersection points with the  -axis (usually it is said that the parabola has just one intersection point); and
-axis (usually it is said that the parabola has just one intersection point); and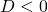 : the parabola has no intersection points with the
: the parabola has no intersection points with the 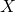 -axis.
-axis.
A parabola is a symmetric graph and has a symmetry axis, namely the line:
![]()
Then it is clear that the top of the parabola is on this symmetry axis:
![]()
This can also be deduced from the ![]() -formula. This optimum can also be found by differentiating the function and make the derivative equal to
-formula. This optimum can also be found by differentiating the function and make the derivative equal to ![]() :
:
![]()
![]()
see also the topic Differentiation of standard functions .
Example 1
Given the function:
![]()
1. Determine the intersection point of the graph with the ![]() -axis;
-axis;
2. Does this graph have an intersection point with the ![]() -axis, and if so, how many and determine their coordinates.
-axis, and if so, how many and determine their coordinates.
3. Determine the symmetry axis.
1. Because ![]() in the formula is equal to
in the formula is equal to ![]() , the intersection point with the
, the intersection point with the ![]() -axis is equal to
-axis is equal to ![]() .
.
2. We have to compute the discriminant:
![]()
![]() is greater than
is greater than ![]() en thus the graph has two intersection points with the
en thus the graph has two intersection points with the ![]() -axis. The
-axis. The ![]() -coordinates of these intersection points are:
-coordinates of these intersection points are:
![]()
so:
![]()
![]()
and the coordinates are:
![]() and
and ![]()
3. The symmetry axis can be calculated in two way. First by using the formula above, but also by taking the mean value of the two intersection points, namely:
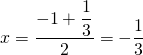
Example 2
Given the function:
![]()
1. Determine the intersection point of the graph with the ![]() -axis;
-axis;
2. Does this graph have an intersection point with the ![]() -axis, and if so, how many and determine their coordinates.
-axis, and if so, how many and determine their coordinates.
3. Determine the symmetry axis.
1. Because ![]() in the formula is equal to
in the formula is equal to ![]() , the intersection point with the
, the intersection point with the ![]() -axis is equal to
-axis is equal to ![]() .
.
2. We can compute the discriminant to find out whether there are one or more intersection points, but another way is faster. The equation can be factorized:
![]()
and thus we may conclude that the graph has two intersection points with the ![]() -axis:
-axis: ![]() en
en ![]() .
.
3. The symmetry axis lies just in the middle of these two points, so the symmetriy-axis is ![]() .
.
Example 3
For which value of ![]() does the parabola:
does the parabola:
![]()
have two coinciding intersection points with the ![]() -axis.
-axis.
These intersection points coincide if the discriminant ![]() , so:
, so:
![]()
![]()

