Absolute value |x|

Summary and examples

The absolute value $f(x)=|x|$ is often seen as ackward. It is defined as follows:

$|x|=x$ if $x\geq0$

$|x|=-x$ if $x<0$

The absolute value indicates the magnitude of $x$ , thus the value of $x$ without a $+$ or $-$ sign.

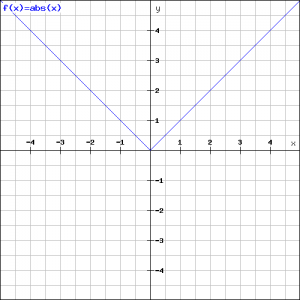
Example 1

As an example, we look at the function $f(x)=|x|$ . According to the definition above we have $f(x)=x$ if $x\geq0$ , so a straight line, and $f(x)=-x$ if $x<0$ .

abs(x)

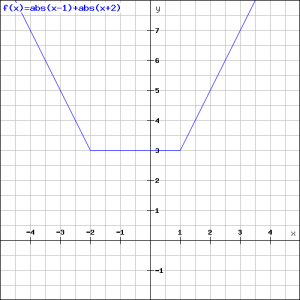
Example 2

Draw the graph of the function:

$f(x)=|x-1|+|x+2|$

According to the definition we have:

$|x-1|=x-1$ if $x\geq1$ , call this case A.

$|x-1|=-(x-1)=-x+1$ if $x<1$ , call this case B.

$|x+2|=x+2$ if $x\geq-2$ , call this case C.

$|x+2|=-(x+2)=-x-2$ if $x<-2$ , call this case D.

Now we consider the following intervals for $x$ .

If $x<-2$ , then the cases B and D hold, so:

$f(x)=-x+1-x-2=-2x-1$

If $-2\leq{x}<1$ , then the cases B and C hold, so:

$f(x)=-x+1+x+2=3$

If $x\geq1$ , then the cases A and C hold, so:

$f(x)=x-1+x+2=2x+1$

The following graph is the result:

abs(x-1)+abs(x+2)

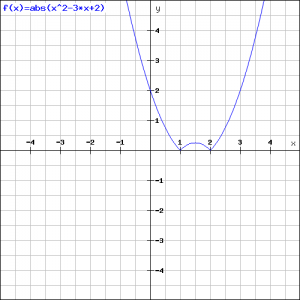
Example 3

Now we apply the absolute value function to a quadratic function:

$f(x)=|x^2-3x+2|$

The graph of the function $x^2-3x+2$ is a parabola with $X$ -intercepts $x=1$ or $x=2$ . The parabola opens up and in the interval $1<x <2$ it will lie below the $X$ -axis. Because the function $f(x)$ relates to the absolute value of this parabola, the negative part will be replaced by the positive equivalent, see the figure.

When this insight is lacking, also the definition of the absolute value can be applied:

$|x^2-3x+2|=x^2-3x+2$ if $x\leq1$ or $x\geq2$

$|x^2-3x+2|=-x^2+3x-2$ if $1<x<2$

abs(x^2-3x+2)

0

Web Design Bangladesh Web Design Bangladesh Mymensingh