Assignments

Quadratic functions are frequently used in mathematics. Therefore it is important to know:

• that the graph of a quadratic function is a parabola;
• when the parabola opens up or down;
• how you can quickly determine the intersection point with the 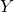-axis; and
• how you can find out whether the parabola has no, one or two intersection points with the 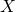-axis and that the discriminant plays an important role.

1. Given the function:

Answer the following questions:

1. What is the intersection point of the graph and the 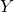-axis?
2. Do the graph and the 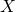-axis have intersection points, and if so, how many?
3. What is the symmetry axis?

Solution

2. Given the function:

Answer the following questions:

1. For which value of 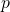does the parabola have no intersection points with the 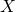-axis?
2. Calculate the intersection point with the 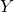-axis.
3. Does the graph has a maximum or a minimum?

Solution

3. Given the function:

Answer the following questions:

1. What is the intersection point of the graph with the 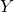-axis?
2. Does the graph have intersection points with the 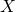-axis, and if so, how many? Calculate the coordinates.
3. What is the symmetry axis?

Solution

4. The equation of a parabola is:

For which value of does the top of this parabola lie on the line:

Solution

5. The -coordinate of the top of the parabola:

is equal to .

Calculate .

Solution

6. For which value of  does the parabola:

have no intersection points with the -axis?

Solution

7. For which value of  does the parabola:

have two intersection points with the -axis having a mutual distance of ?

Solution

8. For which value of  does the top of the parabola:

lie on the line:

Solution

9. Calculate the equation of the parabola going through the points ,  and .

Solution

10. For which value of  do the parabolas:

have just one point in common.

Solution