Quadratic functions and graphs

Summary and examples

The general equation of a quadratic function is:

$y=ax^2+bx+c$

$a$ , $b$ and $c$ are called parameters. $a\neq0$ , because otherwise it is no quadratic function.

The graph of a quadratic function is a parabola. There are two types, one that opens up and one that opens down, depending on the parameter $a$ .

$a>0$ : opens up

$a<0$ : opens down

A parabola intersects the $Y$ -axis in the point $(0,c)$ . You can easily see this, because for any point on the $Y$ -axis we have $x=0$ . When $x=0$ is substituted in the equation we get $y=c$ .

When a parabola intersects the $X$ -axis we can calculate the intersection points in various ways. The $abc$ -formula, explained in Quadratic equations (abc-formula), always gives a solution. Another way is based on factorizing the equation, see the topic Quadratic equations (factorizing). This is faster, though not always possible.

The intersection points can be calculated by applying the $abc$ -formula:

$x_{1,2}=\displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

In this formula the discrriminant plays an important role:

$D=b^2-4ac$

We have:

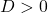$D>0$ : the parabola has two different intersection points with the $X$ -axis;
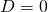$D=0$ : the parabola has two coinciding intersection points with the 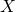$X$ -axis (usually it is said that the parabola has just one intersection point); and
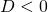$D<0$ : the parabola has no intersection points with the 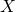$X$ -axis.

A parabola is a symmetric graph and has a symmetry axis, namely the line:

$x=-\displaystyle\frac{b}{2a}$

Then it is clear that the top of the parabola is on this symmetry axis:

$x_{top}=-\displaystyle\frac{b}{2a}$

This can also be deduced from the $abc$ -formula. This optimum can also be found by differentiating the function and make the derivative equal to $0$ :

$y'=2ax+b=0$
$x=-\displaystyle\frac{b}{2a}$

see also the topic Differentiation of standard functions .

Example 1

Given the function:

$y=3x^2+2x-1$

1. Determine the intersection point of the graph with the $Y$ -axis;
2. Does this graph have an intersection point with the $X$ -axis, and if so, how many and determine their coordinates.
3. Determine the symmetry axis.

1. Because $c$ in the formula is equal to $-1$ , the intersection point with the $Y$ -axis is equal to $(0,-1)$ .
2. We have to compute the discriminant:

$D=2^2-4.3.-1=16$

$D$ is greater than $0$ en thus the graph has two intersection points with the $X$ -axis. The $x$ -coordinates of these intersection points are:

$\displaystyle\frac{-2\pm\sqrt{16}}{2.3}=\displaystyle\frac{-2\pm4}{6}$

so:

$x_1=-1$
$x_2=\displaystyle\frac{1}{3}$

and the coordinates are:

$(-1,0)$ and $(\displaystyle\frac{1}{3},0)$

3. The symmetry axis can be calculated in two way. First by using the formula above, but also by taking the mean value of the two intersection points, namely:

$x=\displaystyle\frac{-1+\displaystyle\frac{1}{3}}{2}=-\displaystyle\frac{1}{3}$

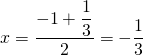
Example 2

Given the function:

$y=x^2-6x+8$

1. Because $c$ in the formula is equal to $8$ , the intersection point with the $Y$ -axis is equal to $(0,8)$ .
2. We can compute the discriminant to find out whether there are one or more intersection points, but another way is faster. The equation can be factorized: