Terug naar Opgaven Raaklijn aan grafiek bepalen
Opgave 7
Bepaal de vergelijking van de raaklijn(en) aan de grafiek van de functie:
die evenwijdig loopt (lopen) aan de raaklijn in het punt 
van de grafiek van de functie:
Uitwerking
We bepalen eerst de richtingscoëfficiënt van de raaklijn in het punt . Daartoe moeten we de tweede functie differentiëren:
In het punt is de richtingscoëfficiënt gelijk aan:
We moeten nu proberen het punt of de punten te vinden op de grafiek van de functie:
waarvan de raaklijn(en) een richtingscoëfficiënt 
heeft (hebben).
Een raaklijn aan deze functie heeft als richtingscoëfficiënt:
en we moeten nu de waarden van 
vinden waarvoor geldt:
of
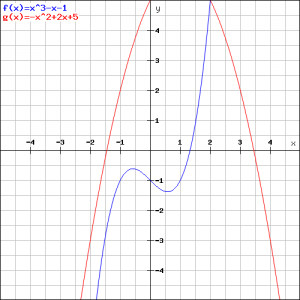
Deze vergelijking heeft geen (reële) oplossingen en dus bestaat de gevraagde raaklijn niet. Dit kan in de onderstaande figuur worden geverifieerd.
Terug naar Opgaven Raaklijn aan grafiek bepalen
