Solution assignment 07 Tangent line to graph

Calculate the equation of the tangent line(s) of the graph of the function:

$y=x^3-x-1$

parallel to the tangent line at the point $P(2,5)$ of the graph of the function:

$y=-x^2+2x+5$

First we calculate the slope of the tangent line at $(2,5)$ . For this we have to differentiate the second function:

$y'=-2x+2$

In the point $(2,5)$ the slope is equal to:

$y'=-2\cdot2+2=-2$

Now we have to try and find the points on the graph of the function:

$y=x^3-x-1$

of which the tangent line(s) has (have) a slope equal to $-2$ .
An tangent line at the graph of this function has a slope:

$y'=3x^2-1$

So we have to find the values of $x$ for which we have:

$3x^2-1=-2$

or:

$x^2=-1$

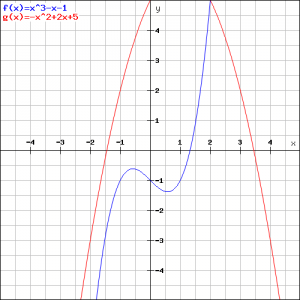
This equation has no (real) solutions and thus the required tangent line(s) does (do) not exist. We can verify this in the figure below.

grafiek