Solution assignment 09 Exponential functions and graphs

Return to Assignments Exponential functions and graphs

Assignment 9

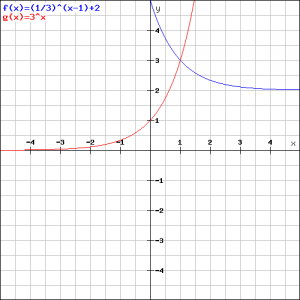
Draw the graphs of the functions:

$f: y=3^x$

$g: y=(\displaystyle\frac{1}{3})^{x-1}+2$

Calculate the intersection point of both graphs.

Solution

We already outlined in previous assignments how the graphs of both functions can be sketched.
To find the intersection point we have to solve the following equation:

$3^x=(\displaystyle\frac{1}{3})^{x-1}+2$

$3^x=(3^{-1})^{x-1}+2$

$3^x=3^{-x+1}+2$

We multiply both sides by $3^x$ and get:

$3^{2x}-2.3^x-3=0$

We transform this equation by substituting:

$y=3^x$

Then we get:

$y^2-2y-3=0$

$(y-3)(y+1)=0$

We solved the quadratic equation by factorizing. The solutions of this equation are: $y=3$ or $y=-1$ . The latter soluton does not satisfy the equation because $y$ is an exponential function and thus positive. Therefore we get the solution from the exponential equation: